Question

Find the value of x that satisfies the given conditions.

The line containing A(4,-2) and B(x,-6) is perpendicular to the line containing C(-2,-9) and D(3,-4)

(please provide explanation, upcoming exam.)

Answer 1

if two lines are perpendicular multiplying their gradients would give -1 (the gradient of one line is the negative reciprocal of the other).

in order to calculate the gradient of the line you would use:

gradient = difference in y / difference in x

so let’s work out the gradient of the line containing point c and d:

gradient = (-4) - (-9) / (3) - (-2)

= 5 / 5 = 1

let’s also work out the gradient of the line containing points a and b in terms of x:

gradient = (-6) - (-2) / (x) - (4)

= -4 / x - 4

so we know that multiplying both gradients should give us -1:

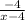`(-4)/(x - 4)`× 1 = - 1

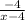`(- 4)/(x - 4)` = - 1

-4 = -x + 4

-x = -8

therefore, x = 8

hope this helps! feel free to ask me if you don’t understand something :)