Question

The Smith family wants to save money to travel the world. They plan to invest in an ordinary annuity that earns 5.4% interest, compounded quarterly. Payments will be made at the end of each quarter.

How much money do they need to pay into the annuity each quarter for the annuity to have a total value of $12,000 after 11 years?
Do not round intermediate computations, and round your final answer to the nearest cent. If necessary, refer to the list of financial formulas.

Answer 1

$201.48

Explanation:

To determine the quarterly payments needed for the annuity to reach a total value of $12,000 after 11 years, we can use the formula for the future value of an ordinary annuity:

`FV=P\left((\left(1+(r)/(n)\right)^(nt)-1)/((r)/(n))\right)`

where:

• FV = Future value of an ordinary annuity.
• P = Value of each payment.
• r = Annual interest rate (in decimal form).
• n = Number of times interest is applied per year.
• t = Time (in years).

Given values:

• FV = $12,000
• r = 5.4% = 0.054
• n = 4 (quarterly)
• t = 11 years

Substitute the values into the formula and solve for P:

`\begin{aligned}12000&=P\left((\left(1+(0.054)/(4)\right)^(4 \cdot 11)-1)/((0.054)/(4))\right)\\\\12000&=P\left(((1+0.0135)^(44)-1)/(0.0135)\right)\\\\12000&=P\left(((1.0135)^(44)-1)/(0.0135)\right)\\\\12000\cdot 0.0135&=P\left((1.0135)^(44)-1}\right)\\\\162&=P\left((1.0135)^(44)-1}\right)\\\\P&=(162)/(\left(1.0135)^(44)-1)\right}\end{aligned}`

Evaluate using a calculator:

`P=201.483584857...`

`P=201.48`

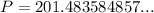
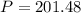
Therefore, the Smith family needs to pay approximately $201.48 into the annuity each quarter to accumulate a total value of $12,000 after 11 years, considering a 5.4% interest rate compounded quarterly.