Question

A triangular field has sides of lengths 41, 76, 113 ft.

Enter your answer as a number; answer should be accurate to 2 decimal places.

Find the largest angle in degrees:

Answer 1

To find the largest angle in the triangular field with sides of lengths 41 ft, 76 ft, and 113 ft, we can use the Law of Cosines. The law states that in a triangle with sides of lengths a, b, and c, and the angle opposite side c denoted as angle C, the following equation holds:

`\displaystyle\sf c^(2) = a^(2) + b^(2) - 2ab \cos(C)`.

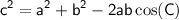In our case, the sides of the triangle are 41 ft, 76 ft, and 113 ft. Let's denote the largest angle as angle C, which is opposite the side of length 113 ft. We can rearrange the equation and solve for the cosine of angle C:

`\displaystyle\sf \cos(C) = (a^(2) + b^(2) - c^(2))/(2ab)`.

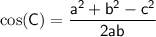Substituting the values of a = 41 ft, b = 76 ft, and c = 113 ft into the equation, we have:

`\displaystyle\sf \cos(C) = (41^(2) + 76^(2) - 113^(2))/(2 \cdot 41 \cdot 76)`.

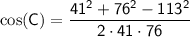Calculating the value, we find:

`\displaystyle\sf \cos(C) \approx -0.6578`.

To find the largest angle C, we take the inverse cosine (arccos) of this value:

`\displaystyle\sf C \approx \arccos(-0.6578)`.

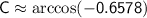Using a calculator, we find:

`\displaystyle\sf C \approx 130.86 \, \text{degrees}`.

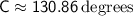Therefore, the largest angle in the triangular field is approximately 130.86 degrees.