Question

Triangle KLM, with vertices K(-5,-8), L(-2,-5), and M(-7,-4), is drawn on the coordinate grid below. What is the area, in square units, of triangle KLM?

Answer 1

Explanation:

K(-5;-8) L(-2;-5) M(-7;-4) SΔKLM=?

The area of a KLM triangle with vertices at points A(x₁;y₁), B(x₂;y₂), C(x₃;y₃) can be calculated using the formula:

`\displaystyle\\S_(KLM)=(1)/(2) *|(x_2-x_1)*(y_3-y_1)-(x_3-x_1)*(y_2-y_1)|`

`x_1=-5\ \ \ \ \ \ x_2=-2\ \ \ \ \ \ x_3=-7\ \ \ \ \ \ y_1=-8\ \ \ \ \ \ y_2=-5\ \ \ \ \ \ y_3=-4`

`\displaystyle\\S _(KLM)=(1)/(2)*|(-2-(-5))*(-4-(-8))-(-7-(-5))*(-5-(-8))|\\\\\\S_(KLM)=(1)/(2)*|(-2+5)*(-4+8)-(-7+5)*(-5+8)|\\\\\\S_(KLM)=(1)/(2) *|3*4-((-2)*3|\\\\\\S_(KLM)=(1)/(2)*|12+6|\\\\\\S_(KLM)=(1)/(2) *|18|\\\\\\S_(KLM)=(18)/(2) \\\\\\S_(KLM)=9 \ square\ units.`

`Answer: \ S_(KLM)=9 \ square\ units.`

Answer 2

9 square units

Explanation:

You want the area of triangle KLM with vertices K(-5, -8), L(-2, -5), and M(-7, -4).

Pick's theorem

For small polygons with vertices on the coordinate grid, the area is conveniently found using the formula ...

A = i + b/2 -1

where i is the number of interior grid points, and b is the number of boundary grid points.

Application

In the attached, we have identified the interior grid points in red. There are 7 of them. The boundary grid points are blue, and there are 6 of them. That means the area is ...

A = 7 +(6/2) -1 = 9

The area of the triangle is 9 square units.

__

Additional comment

The area was also found using the geometry program that drew the triangle. It found the area to be 9 square units.

The area can be found directly from the grid point coordinates as half the absolute value of the sum of determinants of pairs of points.

A = 1/2|((-2)(-4)-(-5)(-7) +(-7)(-8) -(-4)(-5) +(-5)(-5) +(-8)(-2)|

A = 1/2|8 -35 +56 -20 +25 -16| = 1/2|18| = 9 . . . . square units

And, the area can be found from the graph by subtracting the three corner triangle areas from the bounding rectangle area.

A = 5×4 -1/2(5×1 +3×3 +2×4) = 20 -1/2(5 +9 +8) = 9 . . . . square units

The determinant of a pair of points, as used above, is ...

`\left|\begin{array}{cc}a&b\\c&d\end{array}\right|=ad-cb`

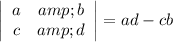
It does not matter whether the point coordinates are written as a row, or as a column. The determinant is the same in either case. What matters is that the points are used in the same order. Above, we used LM, MK, KL as the pairs of points.

<95141404393>