Question

Find the general solution to the differential equation 2y''+2y'+y=0

Answer 1

`y=c_1e^{-(1)/(2)t }\cos((1)/(2)t )+c_2e^{-(1)/(2)t }\sin((1)/(2)t )`

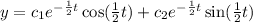
Explanation:

Solve the given differential equation.

`2y''+2y'+y=0`

`\hrulefill`

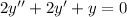
(1) - Find the characteristic equation

For this equation, the characteristic equation is given by:

`2m^2+2m+1=0`

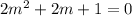
(2) - Solve for "m" using the quadratic formula

`\boxed{\left\begin{array}{ccc}\text{\underline{The Quadratic Formula:}}\\\\m=(-b\pm√(b^2+4ac) )/(2a) \end{array}\right}`

a=2, b=2, c=1

`\Longrightarrow m=(-2\pm√(2^2-4(2)(1)) )/(2(2)) \\\\\\\Longrightarrow m=(-2\pm√(4-8) )/(4) \\\\\\\Longrightarrow m=(-2\pm√(-4) )/(4) \\\\\\\Longrightarrow m=(-2\pm√(4)√(-1) )/(4) \\\\\\\Longrightarrow m=(-2\pm2i )/(4) \\\\\\\Longrightarrow m=(-2)/(4) \pm(2)/(4)i \\\\\\\therefore \boxed{ m=(-1)/(2) \pm(1)/(1)i }`

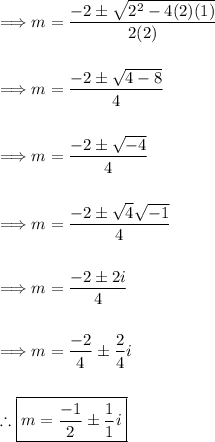
(3) - Form the general solution

`\boxed{\left\begin{array}{ccc}\text{\underline{Solutions to Higher-order DE's:}}\\\\\text{Real,distinct roots} \rightarrow y=c_1e^(m_1t)+c_2e^(m_2t)+...+c_ne^(m_nt)\\\\ \text{Duplicate roots} \rightarrow y=c_1e^(mt)+c_2te^(mt)+...+c_nt^ne^(mt)\\\\ \text{Complex roots} \rightarrow y=c_1e^(\alpha t)\cos(\beta t)+c_2e^(\alpha t)\sin(\beta t)+... \ ;m=\alpha \pm \beta i\end{array}\right}`

We have complex roots, so we can form the solution as:

`\boxed{\boxed{y=c_1e^{-(1)/(2)t }\cos((1)/(2)t )+c_2e^{-(1)/(2)t }\sin((1)/(2)t )}}`

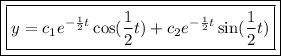
Thus, the problem is solved.