Question

Consider the function f (x) = x4 − 18x2 +10,

−2student submitted image, transcription available belowxstudent submitted image, transcription available below7.
Find the absolute minimum value of this function.
ALSO,
Find the absolute maximum value of this function.

Answer 1

maximum: 10

minimum: -71

Explanation:

The absolute minimum and maximum points of a function are the points where the instantaneous slope, or derivative, is 0.

To find these points, we first need find the general form for the derivative of the function:

`f(x) = x^4 - 18x^2+10`

↓ applying the sum/difference rule ...
`\left[ \frac{}{}f(x) \pm g(x)\frac{}{}\right]' = f'(x) \pm g'(x)`

`f'(x) = (x^4)' - (18x^2)' + (10)'`

↓ applying the power rule ...
`(x^a)' = ax^((a-1))`

`f'(x) = 4x^3 - 18(2x) + 0`

`f'(x) = 4x^3 - 36x`

Now, we can plug in 0 for f'(x) to find the minimum and maximum points.

`0 = 4x^3 - 36x`

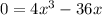
↓ factoring a 4x out of the right side

`0 = 4x(x^2 - 9)`

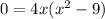
↓ applying the difference of squares formula ...
`x^2 - a^2 = (x + a)(x - a)`

`0 = 4x(x + 3)(x - 3)`

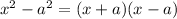
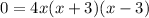
↓ splitting into 3 equations ...
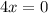`\text{if } ABC = 0,\text{ then } A = 0 \text{ or } B=0 \text{ or } C = 0`

`4x = 0` or
`x + 3 = 0` or
`x-3=0`

`x = 0` or
`x = -3` or
`x = 3`

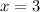
Finally, we can plug these x-values back into the function to find the function's maximum and minimum y-values.

when x = 0...

`f(0) = 0^4 - 18(0^2)+10`

`f(0) = 10`

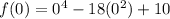
when x = -3...

`f(-3) = (-3)^4 - 18(-3)^2 + 10`

`f(-3) = 81 - 162 + 10`

`f(-3) = -71`

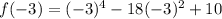
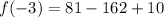
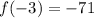
when x = 3...

`f(3) = (3)^4 - 18(3)^2 + 10`

`f(3) = 81 - 162 + 10`

`f(3) = -71`

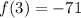
So, the maximum y-value of the function is 10 and the minimum y-value is -71.