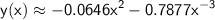To solve the Cauchy-Euler equation \[ x^{2} y^{\prime \prime}+2 x y^{\prime}-6 y=0 \] we can assume a solution of the form
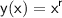 .
.
First, let's find the derivatives of
 :
:
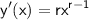
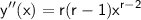
Now, we substitute these expressions back into the original equation:
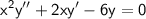

Simplifying the equation:
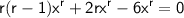

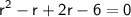
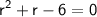
Now we can solve this quadratic equation for
 :
:
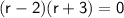
This gives us two possible values for
 :
:
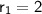

Therefore, the general solution to the Cauchy-Euler equation is given by:
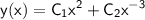
To find the particular solution that satisfies the initial conditions
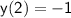 and
and
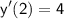 , we substitute these values into the general solution and solve for the constants
, we substitute these values into the general solution and solve for the constants
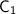 and
and
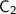 .
.
Substituting
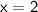 and
and
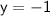 :
:

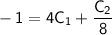
Substituting
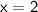 and
and
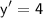 :
:
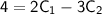
Now we have a system of linear equations that we can solve. Multiplying the first equation by 8 to eliminate fractions:
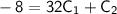
Adding this
equation to the second equation:

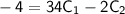
Solving for
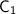 :
:

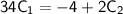
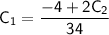
Substituting this value of
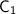 back into the first equation:
back into the first equation:
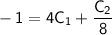
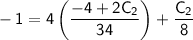
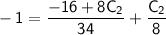
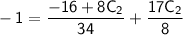


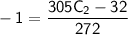
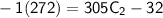
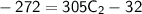
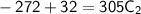

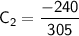
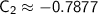
Substituting this value of
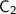 back into the equation for
back into the equation for
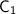 :
:
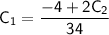
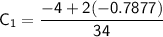
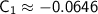
Therefore, the particular solution that satisfies the initial conditions is: