To remove the discontinuity at
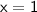 , we need to find the new value
, we need to find the new value
 should be assigned.
should be assigned.
Given the function
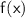 :
:
To remove the discontinuity at
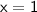 , we need to ensure that the left-hand limit and the right-hand limit of
, we need to ensure that the left-hand limit and the right-hand limit of
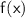 at
at
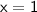 are equal.
are equal.
The left-hand limit is obtained by evaluating
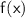 as
as
 approaches
approaches
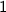 from the left:
from the left:
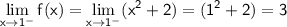
The right-hand limit is obtained by evaluating
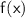 as
as
 approaches
approaches
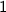 from the right:
from the right:
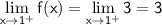
Since the left-hand limit and the right-hand limit are both equal to
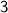 , we can assign
, we can assign
 the value of
the value of
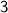 to remove the discontinuity.
to remove the discontinuity.
Therefore, the new value for
 should be
should be
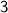 .
.

♥️
