Question

9.17 Two voltages u₁ and U₂ appear in series so that their TT/3) V sum is U = U₁ + 0₂ Kfv, = 10 cos(507 and U₂ = 12 cos(50r +30°) V, find u.

Answer 1

To find the sum of the voltages
`\displaystyle U_(1)` and
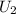`\displaystyle U_(2)` in series, we can use the formula:

`\displaystyle U=U_(1)+U_(2),`

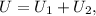
where
`\displaystyle U_(1)` and
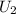`\displaystyle U_(2)` are the given voltages.

Given:
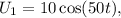`\displaystyle U_(1)=10\cos(50t),` and
`\displaystyle U_(2)=12\cos(50t+30^(\circ))`.

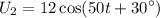Substituting the given values into the equation, we have:

`\displaystyle U=10\cos(50t)+12\cos(50t+30^(\circ)).`

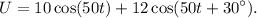
Now, we can simplify the expression by using the trigonometric identity:

`\displaystyle \cos(A+B)=\cos A\cos B-\sin A\sin B.`

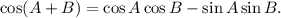
Applying this identity to the equation, we get:

`\displaystyle U=10\cos(50t)+12(\cos(50t)\cos(30^(\circ))-\sin(50t)\sin(30^(\circ))).`

Simplifying further, we have:

`\displaystyle U=10\cos(50t)+12\cos(50t)\cos(30^(\circ))-12\sin(50t)\sin(30^(\circ)).`

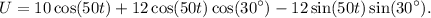
Using the values of
`\displaystyle \cos(30^(\circ))=(√(3))/(2)` and
`\displaystyle \sin(30^(\circ))=(1)/(2)`, we can rewrite the equation as:

`\displaystyle U=10\cos(50t)+12\cos(50t)\left( (√(3))/(2)\right) -12\sin(50t)\left( (1)/(2)\right).`

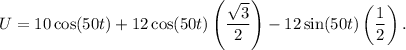
Simplifying further, we have:

`\displaystyle U=10\cos(50t)+6√(3)\cos(50t)-6\sin(50t).`

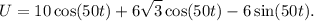
Now, we can combine the terms with the same trigonometric function:

`\displaystyle U=( 10+6√(3))\cos(50t)-6\sin(50t).`

Hence, the sum of the voltages
`\displaystyle U_(1)` and
`\displaystyle U_(2)` is given by:

`\displaystyle U=( 10+6√(3))\cos(50t)-6\sin(50t).`

`\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}`

♥️
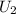`\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}`