To find the arc length of the curve
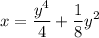 on the interval
on the interval
 , we can use the arc length formula for a curve given by
, we can use the arc length formula for a curve given by
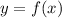 :
:

where
 and
and
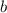 are the corresponding x-values of the interval
are the corresponding x-values of the interval
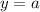 and
and
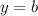 , and
, and
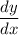 is the derivative of
is the derivative of
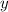 with respect to
with respect to
 .
.
First, let's find the derivative of
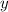 with respect to
with respect to
 :
:
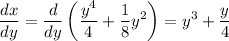 .
.
Now, we can calculate the arc length using the given interval
 :
:
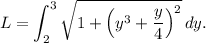
This integral represents the arc length of the curve. Evaluating this integral will give us the desired result. However, this integral does not have a closed-form solution and must be numerically approximated using methods such as numerical integration or calculus software.