Question

at very low temperatures, heat capacity, , is directly proportional to 3 for most substances. write an expression for the absolute molar entropy, , at a low temperature, , in terms of .

Answer 1

The expression for the absolute molar entropy at a low temperature can be written as S = α ∫(Cp/T)dT, where Cp is the heat capacity and α is a constant.

Step-by-step explanation:

The absolute molar entropy, S, at a low temperature, T, can be expressed in terms of the heat capacity, Cp, by integrating the ratio q/T from 0 K to T. At very low temperatures, heat capacity, Cp, is directly proportional to T^3 for most substances. Therefore, we can write the expression for the absolute molar entropy, S, at a low temperature, T, as:

S = α ∫(Cp/T)dT

where α is a constant that depends on the substance and the units used.

Answer 2

The absolute molar entropy (S) at a low temperature (T) for most substances can be calculated by integrating the heat capacity (Cp) over temperature, using Cp = a
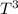`T^3` here 'a' is a constant).

Step-by-step explanation:

In the context of low temperatures, it is observed that the heat capacity (Cp) of most substances is directly proportional to the cube of the temperature (T3). According to the third law of thermodynamics, the absolute molar entropy (S) can be determined by integrating the heat capacity over temperature from absolute zero to the temperature of interest. Specifically, S is found by the area under the Cp/T vs T curve from 0 K to a given temperature T.

To write an expression for S at a low temperature T, in terms of Cp, the relationship Cp =
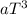`aT^3` 'a' is a constant) can be used. Therefore, the expression for absolute molar entropy, assuming the validity of the Debye approximation, is given by the integral:

S = ∫(0, T) (aT3) / T dT = a ∫(0, T) T2 dT = aT3 / 3