Question

A voltage 100 sin wt + 40 cos (3 wt -30°) + 50 sin (5ot + 45°) V is applied to the pressure coil circuit of a wattmeter and through the current coil is passed a current of 8 sin oot + 6 cos (5 wt-120°) A.

Answer 1

In this problem, we are given the voltage and current expressions for an AC circuit. We need to find the amplitude and phase angle of the current in order to analyze the circuit.

Step-by-step explanation:

AC Circuit Analysis

In this problem, we are given the voltage and current expressions for an AC circuit. The voltage expression is given as 100 sin(wt) + 40 cos(3wt - 30°) + 50 sin(5wt + 45°) V, and the current expression is given as 8 sin(wt) + 6 cos(5wt - 120°) A.

To analyze the circuit, we need to find the amplitude and phase angle of the current. The amplitude, Io, can be found by taking the square root of the sum of the squares of the coefficients of the sine and cosine terms. The phase angle, θ, can be found by taking the arctan of the coefficient of the cosine term divided by the coefficient of the sine term.

Using these formulas, we can find the values of Io and θ for the given current expression, and then use them to analyze the circuit.

Answer 2

So, the amplitude
`\(I_0\)` is
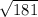`\(√(181)\)` and the phase angle
`\(\phi\)` is given by the arctangent of the ratio of the coefficients of the sine and cosine terms.

Let's express the given current in the form
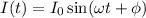`\(I(t) = I_0 \sin(\omega t + \phi)\)` and find the amplitude
`\(I_0\)` and the phase angle
`\(\phi\)`.

Given current:

`\[ I(t) = 8 \sin(\omega t) + 6 \cos(5 \omega t - 120^\circ) \, \text{A} \]`

Let's use trigonometric identities to rewrite the current expression in the desired form:

`\[ I(t) = I_0 \sin(\omega t + \phi) \]`

Comparing coefficients, we have:

1. For the term
`\(8 \sin(\omega t)\), \(I_0 = 8\)`, and there is no phase shift
`(\(\phi = 0\))`.

2. For the term
`\(6 \cos(5 \omega t - 120^\circ)\), \(I_0 = 6\) and \(\phi = 120^\circ\)`.

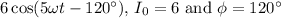So, the current expression becomes:

`\[ I(t) = 8 \sin(\omega t) + 6 \cos(5 \omega t - 120^\circ) \]\[ I(t) = 8 \sin(\omega t) + 6 \cos(5 \omega t - 120^\circ) \]\[ I(t) = 8 \sin(\omega t) + 6 \cos(5 \omega t) \cdot \cos(120^\circ) - 6 \sin(5 \omega t) \cdot \sin(120^\circ) \]\[ I(t) = 8 \sin(\omega t) - 3 \cos(5 \omega t) - 6 √(3) \sin(5 \omega t) \]`

Now, let's combine the sine and cosine terms:

`\[ I(t) = A \sin(\omega t + \phi) \]`

Where:

`\[ A = \sqrt{8^2 + (-3)^2 + (-6√(3))^2} = √(64 + 9 + 108) = √(181) \]\[ \phi = \arctan\left((-6√(3))/(8)\right) \]`

Complete the question:

A voltage 100 sin wt + 40 cos (3 wt -30°) + 50 sin (5ot + 45°) V is applied to the pressure coil circuit of a wattmeter and through the current coil is passed a current of 8 sin oot + 6 cos (5 wt-120°) A. Find the amplitude and phase angle of the current in order to analyze the circuit.