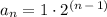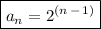Answer:

Explanation:
The general form for a geometric sequence is:
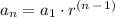
where
 is the
is the
 th term in the sequence,
th term in the sequence,
 is the 1st term, and
is the 1st term, and
 in the common ratio between any two consecutive terms.
in the common ratio between any two consecutive terms.
In this sequence:
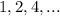
we can identify the common ratio as:
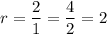
We are also given that the first term is:
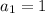
Hence, we can plug these values into the general form for a geometric sequence to get the explicit formula for the given sequence: