The left Riemann sum underestimates the area, giving a value of 24.5, while the right Riemann sum overestimates the area, giving a value of 38.5. The actual area lies somewhere between these two values. Therefore, we can estimate that the area is between 24.5 and 38.5 square units.
We can approximate the definite integral using two different Riemann sums:
Left Riemann Sum: This sum uses the left Riemann endpoints of each subinterval.
Right Riemann Sum: This sum uses the right Riemann endpoints of each subinterval.
Divide the interval into subintervals: We are given that we should use 4 rectangles, so the width of each subinterval will be:
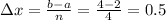
Calculate the Riemann sums:
Left Riemann Sum:
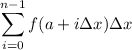
Right Riemann Sum:
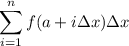
Left Riemann Sum:

Right Riemann Sum:
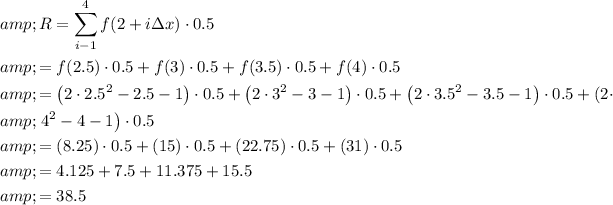
Complete Question:
Use left and right endpoints and the given number of rectangles to find two approximations of the area of the region between the graph of the function and the x-axis over the given interval.
g(x)=2 x^2-x-1,[2,4], 4 rectangles
? < Area < ?