Question

What is the minimum photon energy necessary to dissociate

2H? Take the binding energy to be 2.224589 MeV

Answer 1

The minimum photon energy necessary to dissociate ²H (deuterium) is 2.224589 MeV.

Step-by-step explanation:

The minimum photon energy required to dissociate a nucleus is given by the difference between the binding energy of the nucleus and the energy of the separated nucleons. For deuterium (²H), which consists of one proton and one neutron, the binding energy is given as 2.224589 MeV.

To dissociate it into its constituent nucleons, we need to provide energy equal to the binding energy. Therefore, the minimum photon energy (
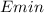`E min`) required is 2.224589 MeV.

This concept is rooted in Einstein's mass-energy equivalence principle (E=mc²), where the energy required to break the binding forces between nucleons is equivalent to the mass lost in the process. The binding energy represents the energy released when nucleons come together to form a nucleus, and to break them apart, an equivalent amount of energy must be supplied.

In the case of deuterium, the minimum photon energy needed for dissociation is the binding energy, which is 2.224589 MeV.

In nuclear physics, understanding the energy required for nuclear reactions is crucial for various applications, including nuclear energy production and understanding astrophysical processes. The calculation of minimum photon energy provides insights into the stability and behavior of atomic nuclei under different conditions.

Answer 2

The minimum photon energy required to dissociate deuterium (2H) is equal to its binding energy, which is 2.224589 MeV.

Step-by-step explanation:

The minimum photon energy required to dissociate 2H (Deuterium) can be determined by considering the binding energy of the nucleus. The binding energy is the amount of energy needed to break apart the nucleus into its constituent protons and neutrons. For deuterium, this energy is equivalent to the binding energy of the nucleus, which is given as 2.224589 MeV (Mega electron-Volts). Therefore, a photon must have at least this much energy to cause dissociation.