Question

A circle has a radius of 11 ft. Find the radian measure of the central angle A degrees that intercepts an arc of length 5 ft. Do not round any intermediate computations, and round your answer to the nearest tenth.

Answer 1

The answer is
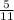`(5)/(11)\\` = 0.45; rounded up(to the nearest tenth) is 0.5

Explanation:

The angle measure of a circle in radians is 2
`\pi`.

First, find the circumference of the circle in terms of
`\pi`.

The formula for the circumference of a circle is 2
`\pi`r (2 ×
`\pi` × radius)

Then find the ratio of the arc length of the central angle to the circumference.

Arc length of the central angle = 5.

Circumference = 22
`\pi`

The ratio of the arc length of the central angle to the circumference is equal to
`(5)/(22\pi )`

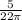
Now use that ratio to find the central angle in radians by multiplying it by the angle measure of the circle in radians.

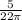`(5)/(22\pi )` × 2
`\pi` = 5/11

Round to the nearest tenth:

`(5)/(11)` ≈ 0.4545 = 0.5