Question

A landfill is leaking leachate with a chloride concentration of 725 mg/L, which enters an aquifer with the following properties: Property Value Hydraulic conductivity=k= 3.0 x 10^-3 cm/s Hydraulic gradient, dh/dl=0.0020 Effective porosity=ne=0.23 Dispersion Coefficient = D*=1.0 x 10^-9 m2/s Compute the chloride concentration after 1 year at distance of 15 m from the source of contamination.

Answer 1

To calculate the chloride concentration after 1 year at a distance of 15 m from the source of contamination, you can use the advection-dispersion equation in groundwater flow and transport.

Step-by-step explanation:

To calculate the chloride concentration after 1 year at a distance of 15 m from the source of contamination, we can use the advection-dispersion equation in groundwater flow and transport. The advection-dispersion equation is given by:

C = C0 * exp(-vx/L) * (exp(2D*t/L^2) - 1)

Where:

• C is the concentration of the contaminant at the distance x.
• C0 is the initial concentration of the contaminant.
• v is the velocity of the groundwater flow.
• L is the distance from the source of contamination.
• D is the dispersion coefficient.
• t is the time.

Given the values:

• C0 = 725 mg/L
• L = 15 m
• D = 1.0 x 10^-9 m^2/s
• t = 1 year = 365 days = 31,536,000 seconds

And assuming a constant velocity of groundwater flow and neglecting any attenuation reactions, we can calculate the concentration using the given values:

• v = k * dh/dl = (3.0 x 10^-3 cm/s) * 0.0020 = 6.0 x 10^-6 cm/s
• L = 15 m = 1500 cm

Substituting these values into the equation:

C = (725 mg/L) * exp(-(6.0 x 10^-6 cm/s)(1500 cm)/(1500 cm)) * (exp(2(1.0 x 10^-9 m^2/s)(31,536,000 s)/(1500 cm)^2) - 1)

By evaluating this equation, we can find the chloride concentration after 1 year at a distance of 15 m from the source of contamination.

Answer 2

The chloride concentration after 1 year at a distance of 15 m from the landfill source is approximately 723.5 mg/L. The calculation involves the advection-dispersion equation, considering hydraulic conductivity, hydraulic gradient, and dispersion coefficient. The resulting concentration accounts for the transport of contaminants in the aquifer.

Explaination:

The transport of contaminants in groundwater can be modeled using the advection-dispersion equation. The one-dimensional advection-dispersion equation for solute transport is given by:

`\[ (\partial C)/(\partial t) = -(\partial)/(\partial x)(vC) + D^*(\partial^2 C)/(\partial x^2) \]`

where:

-
`\( C \)`is the concentration of the solute,

`- \( t \)`is time,

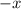`- \( x \)` is the distance along the flow path,

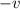`- \( v \)`is the average linear groundwater velocity,

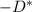`- \( D^* \)`is the dispersion coefficient.

`In this case, the velocity \( v \) is given by \( v = k \cdot (dh)/(dl) \), where \( k \) is the hydraulic conductivity, and \( (dh)/(dl) \) is the hydraulic gradient.`

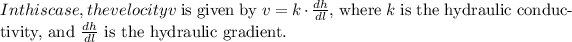
To solve this equation, we can use the method of characteristics. The solution for a pulse input of concentration at time
`\( t = 0 \) and distance \( x = 0 \)` is given by:

`\[ C(x, t) = (C_0)/(2√(\pi D^* t)) \exp\left(-((x-vt)^2)/(4D^*t)\right) \]`

where
`\( C_0 \)` is the initial concentration.

Now, let's calculate the concentration at
`\( x = 15 \ \text{m} \) after \( t = 1 \ \text{year} = 31,536,000 \ \text{seconds} \).`

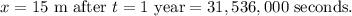
Given values:

`- \( C_0 = 725 \ \text{mg/L} \),- \( k = 3.0 * 10^(-3) \ \text{cm/s} \),- \( (dh)/(dl) = 0.0020 \),- \( D^* = 1.0 * 10^(-9) \ \text{m}^2/\text{s} \).`

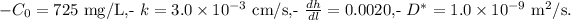
First, convert the units to be consistent:

`\[ v = k \cdot (dh)/(dl) = (3.0 * 10^(-3) \ \text{cm/s}) * 0.0020 \]\[ t = 1 \ \text{year} = 31,536,000 \ \text{seconds} \]`

Now, substitute these values into the concentration equation:

`\[ C(15 \ \text{m}, 31,536,000 \ \text{seconds}) = \frac{725}{2\sqrt{\pi * 1.0 * 10^(-9) * 31,536,000}} \exp\left(-((15 - v * 31,536,000)^2)/(4 * 1.0 * 10^(-9) * 31,536,000)\right) \]`

Calculate this expression to find the chloride concentration after 1 year at a distance of 15 m from the source of contamination.