Question

1. sin(2x - 30°) = cos(x - 10°)

2. 4sinx . cosx - 3sin^2x = 0

please help with this, i have an exam tomorrow and i don’t know how to do this

Answer 1

1) x = 43.33

2) x = tan⁻¹(4/3) = 53.13

Explanation:

1) Formula: cos(A) = sin(90 - A)

sin(2x - 30) = cos(x - 10)

⇒ sin(2x - 30) = sin(90 - (x - 10))

⇒ sin(2x - 30) = sin(90 - x + 10)

⇒ sin(2x - 30) = sin(100 - x)

⇒ 2x - 30 = 100 - x

⇒ 3x = 130

⇒ x = 130/3

x = 43.33

2) 4sinx . cosx - 3sin²x = 0

⇒ 4sinx . cosx = 3sin²x

⇒ 4cosx = 3sinx

⇒
`(4)/(3) =(sinx)/(cosx)`

⇒
`tan x = (4)/(3)`

⇒ x = tan⁻¹(4/3)

⇒ x = 53.13

Answer 2

`\textsf{1)} \quad x \approx 43.33^(\circ)`

`\textsf{2)} \quad \boxed{\begin{aligned}x &= \pi n \;\text{radians}\\x&=0.93+\pi n\; \text{radians}\end{aligned}}\quad \boxed{\begin{aligned}x &= 180^(\circ)n\\x&=53.13^(\circ)+180^(\circ) n\; \end{aligned}}`

Explanation:

Question 1

Given trigonometric equation:

`\sin(2x - 30^(\circ)) = \cos(x - 10^(\circ))`

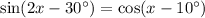
To solve the given trigonometric equation, we can use the following trigonometric identity:

`\boxed{\begin{minipage}{4 cm}\underline{Trigonometric identity} \\\\$\cos (\theta)=\sin(90^(\circ)-\theta)$\\\end{minipage}}`

Apply the trigonometric identity to the right side of the equation:

`\begin{aligned}\sin(2x - 30^(\circ)) &= \cos(x - 10^(\circ))\\\\&= \sin(90^(\circ)-(x - 10^(\circ)))\\\\&= \sin(90^(\circ)-x +10^(\circ))\\\\&= \sin(100^(\circ)-x)\end{aligned}`

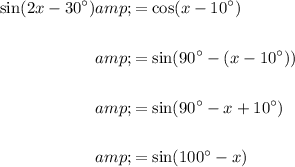
Since the sine function is equal, we can equate the angles:

`2x - 30^(\circ)=100^(\circ)-x`

Now simplify and solve for x:

`\begin{aligned}2x - 30^(\circ)&=100^(\circ)-x\\\\2x - 30^(\circ)+x&=100^(\circ)-x+x\\\\3x - 30^(\circ)&=100^(\circ)\\\\3x - 30^(\circ)+30^(\circ)&=100^(\circ)+30^(\circ)\\\\3x&=130^(\circ)\\\\(3x)/(3)&=(130^(\circ))/(3)\\\\x&=\left((130)/(3)\right)^(\circ)\\\\x&\approx 43.3^(\circ)\; \sf (nearest\;tenth)\end{aligned}`

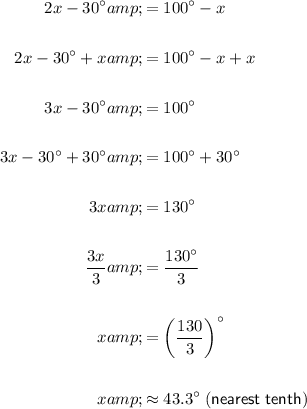
Therefore, the solution to the equation sin(2x - 30°) = cos(x - 10°) is approximately x = 43.33°.

`\hrulefill`

Question 2

Given trigonometric equation:

`4 \sin x \cos x-3\sin^2x=0`

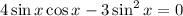
Factor out the common term sin(x):

`\sin x(4 \cos x-3\sin x)=0`

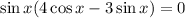
According to the zero product property, one of the factors must be equal to zero for the equation to hold.

Set each factor equal to zero and solve for x.

Factor 1

`\sin x=0`

According to the unit circle, sin(x) = 0 when x = 0 and x = π.

As the sine function is periodic with a period of 2π, the solutions to sin(x) = 0 are:

`x=0+2\pi n, \;\;x=\pi + 2\pi n`

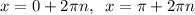
Therefore, x is any multiple of π, where n is an integer:

`\boxed{x = \pi n}`

Factor 2

`\begin{aligned}4\cos x - 3 \sin x & = 0\\\\4 \cos x & = 3 \sin x\\\\(4)/(3)&=(\sin x)/(\cos x)\\\\(4)/(3)&=\tan x\\\\\implies x&=\arctan\left((4)/(3)\right)\\\\x&=0.92729...\end{aligned}`

As the tangent function is periodic with a period of π, the solutions are:

`\boxed{x=0.92729...+\pi n}`

where n is an integer.

Therefore, the solutions to the equation 4sin(x)cos(x) - 3sin²(x) = 0 are:

`\boxed{\begin{aligned}x &= \pi n \;\text{radians}\\x&=0.93+\pi n\; \text{radians}\end{aligned}}`
`\boxed{\begin{aligned}x &= 180^(\circ)n\\x&=53.13^(\circ)+180^(\circ) n\; \end{aligned}}`

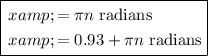
(where n is an integer)