Question

A Web music store offers two versions of a popular song. The size of the standard version is 2.8 megabytes (MB). The size of the high-quality version is 4.3 MB. Yesterday, there were 870 downloads of the song, for a total download size of 3381 MB. How many downloads of the standard version were there? b music store offers two versions of a popular song. The size of the standard version is 2.8 megabytes (MB). The size of the high-quality version is 4.3 MB. Yesterday, there were 870 downloads of the song, for a total download size of 3381 MB. How many downloads of the standard version were there?

Answer 1

240 standard versions of the song were downloaded

(and 630 high-quality versions of the song were downloaded)

Explanation:

Let the downloads of the standard version be x

And the downloads of the high-quality version be y

Since the total downloads were 870, so we get,

x + y = 870 (i)

Also, The total download size was 3381 MB

Meaning the size of the high-quality downloads + the size of the standard version downloads = 3381

so,

Solving these to get x and y,

`x + y = 870 \ \ \ (i)\\2.8x + 4.3y = 3381 \ \ \ (ii)`

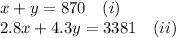
Using (i), we get,

x = 870 - y

putting this value of x into (ii), we get,

`(2.8)x + 4.3y = 3381\\(2.8)(870 -y) + 4.3y = 3381\\2436 - 2.8y+4.3y=3381\\1.5y+2436=3381\\1.5y=3381-2436\\1.5y=945\\y=945/1.5\\\\y=630`

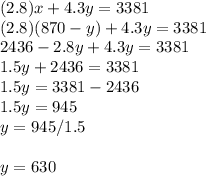
Putting this into the equation,

x = 870 - y, we get,

x = 870 - 630

x = 240

Hence, 240 standard versions of the song were downloaded and 630 high-quality versions of the song were downloaded