Question

Factorize 2(x+y)-x^2+y^2​

Answer 1

(x + y)(2 - x + y)

Explanation:

From the expression, we can rewrite to:

`\displaystyle{2(x+y)-(x^2-y^2)}`

From x² - y², we can apply the difference of two squares law where:

`\displaystyle{x^2-y^2=(x+y)(x-y)}`

Thus,

`\displaystyle{2(x+y)-(x^2-y^2) = 2(x+y)-(x+y)(x-y)}}`

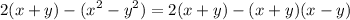
In the expression of 2(x+y) - (x+y)(x-y), there is the same (x+y). Factor (x+y) out of the expression, therefore:

`\displaystyle{2(x+y)-(x+y)(x-y)}\\\\\displaystyle{= (x+y)\left[2-(x-y)\right]}\\\\\displaystyle{=(x+y)(2-x+y)}`

Hence, the factored expression is (x + y)(2 - x + y)