Question

the same force f pushes in three different ways on a box moving with a velocity v, as the drawings show. rank the work done by the force f in ascending order (smallest first).

Answer 1

Without specific details on the force orientations, it's challenging to provide an exact ranking. However, assuming the force is applied parallel to the motion in all cases, the work done is directly proportional to the displacement. Therefore, the work done would be ranked based on the magnitude of the displacements: smallest displacement results in the least work done, and vice versa.

Step-by-step explanation:

The three different ways the force F pushes on the box, but they are not provided in your question. Without specific information about the nature of the force and its application in each scenario, it's challenging to rank the work done accurately.

Work (W) is defined as the product of force (F) and displacement (d) in the direction of the force. Mathematically, it can be expressed as:

`\[ W = F \cdot d \cdot \cos(\theta) \]`

Where:

( W ) is the work done,

( F ) is the magnitude of the force,

( d ) is the displacement, and

`\( \theta \)` is the angle between the force and the direction of displacement.

To rank the work done, you would need to consider the angle between the force and the direction of motion in each case. If the force is applied in the direction of motion
`(\( \theta = 0^\circ \))`, the work done is maximized. If the force is perpendicular to the direction of motion
`(\( \theta = 90^\circ \))`, the work done is zero. If the force opposes the direction of motion
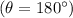`(\( \theta = 180^\circ \))`, the work done is negative.