Question

rock is thrown straight up with an initial speed of 24.0 m/s. Neglect air resistance. (a) At t = 1.0 s, what are the directions of the velocity and acceleration of the rock? Is the speed of the rock increasing or decreasing? (b) At t = 3.0 s, what are the directions of the veloc- ity and acceleration of the rock? Is the speed of the rock increasing or decreasing?

Answer 1

At
`t = 1.0\; {\rm s}`, velocity of the rock points upward (approximately
`14.2\; {\rm m\cdot s^(-1)}`.) Speed of the rock is decreasing.

At
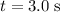`t = 3.0\; {\rm s}`, velocity of the rock points downwards (approximately
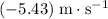`(-5.43)\; {\rm m\cdot s^(-1)}`.) Speed of the rock is increasing.

(Assuming that
`g = 9.81\; {\rm m\cdot s^(-1)}`.)

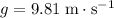Step-by-step explanation:

Let upward be the positive direction. Quantities will be positive if and only if they point upward, and negative if and only if they point downward.

The rock is in a free fall under the influence of gravity. Acceleration of the rock would be
`a = (-g) = (-9.81)\; {\rm m\cdot s^(-2)}` during the entire flight. Note that acceleration
`a` is negative since it points downwards.

The velocity of the rock initially points upwards and is positive. However, under the influence of the negative acceleration, velocity of the rock becomes less positive over time and eventually turns negative (pointing downward) .

The velocity of the rock after a given amount of time
`t` can be found with the SUVAT equation:

`v = u + a\, t`,

Where:

• 
  `u = 24.0\; {\rm m\cdot s^(-1)}` is the initial velocity of the rock at
  `t = 0`, and
• 
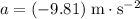  `a = (-9.81)\; {\rm m\cdot s^(-2)}` is the acceleration of the rock.

At
`t = 1.0\; {\rm s}`, velocity of the rock would be:

`\begin{aligned} & 24.0\; {\rm m\cdot s^(-1)} + (1.0\; {\rm s}) \, (-9.81)\; {\rm m\cdot s^(-2)} \\ \approx \; & 14.2\; {\rm m\cdot s^(-1)}\end{aligned}`.

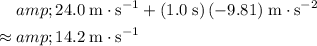The value of velocity is positive, meaning that it points upward.

At
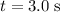`t = 3.0\; {\rm s}`, velocity of the rock would be:

`\begin{aligned} & 24.0\; {\rm m\cdot s^(-1)} + (3.0\; {\rm s}) \, (-9.81)\; {\rm m\cdot s^(-2)} \\ \approx \; &(-5.4)\; {\rm m\cdot s^(-1)}\end{aligned}`.

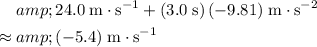The value of velocity is negative, meaning that it points downward.

The speed of an object is equal to the magnitude of its velocity. Refer to the diagram attached:

• As the rock goes upward (first half of each plot,) velocity becomes less positive and approaches
  `0` while speed decreases.
• Speed is
  `0` at the top of the trajectory.
• As the rock goes downward (second half of each plot,) velocity becomes more negative. Speed of the rock increases.

At
`t = 1.0\; {\rm s}`, velocity of the rock is positive (first half of the plot) and the rock is going upward. Speed of the rock would be decreasing.

At
`t = 3.0\; {\rm s}`, velocity of the rock is negative (second half of the plot) and the rock is going downward. Speed of the rock would be increasing.