Question

if the degree measure of an arc of a circle is increased by and the radius of the circle is increased by , by what percent does the length of the arc increase?

Answer 1

If the degree measure of an arc of a circle is increased by
`\displaystyle x\%` and the radius of the circle is increased by
`\displaystyle y\%`, we need to determine the percent by which the length of the arc increases.

Let's assume the original degree measure of the arc is
`\displaystyle D`, and the original radius of the circle is
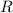`\displaystyle R`. The length of the arc is given by the formula:

`\displaystyle \text{{Arc Length}}=2\pi R\left( \frac{{D}}{{360}}\right)`

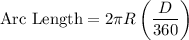
If the degree measure is increased by
`\displaystyle x\%`, the new degree measure would be
`\displaystyle D+D\left( \frac{{x}}{{100}}\right) =D\left( 1+\frac{{x}}{{100}}\right)`.

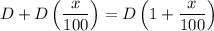If the radius is increased by
`\displaystyle y\%`, the new radius would be
`\displaystyle R+R\left( \frac{{y}}{{100}}\right) =R\left( 1+\frac{{y}}{{100}}\right)`.

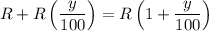The new length of the arc, denoted as
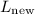`\displaystyle L_{\text{{new}}}`, can be calculated using the new degree measure and radius:

`\displaystyle L_{\text{{new}}}=2\pi \left( R\left( 1+\frac{{y}}{{100}}\right)\right) \left( \frac{{D\left( 1+\frac{{x}}{{100}}\right)}}{{360}}\right)`

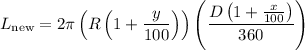
To determine the percent increase in the length of the arc, we can calculate the percentage difference between the new length
`\displaystyle L_{\text{{new}}}` and the original length
`\displaystyle L`:

`\displaystyle \text{{Percent Increase}}=\frac{{L_{\text{{new}}}-L}}{{L}}* 100`

Now, we can substitute the expressions for
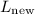`\displaystyle L_{\text{{new}}}` and
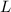`\displaystyle L` into the formula and simplify to determine the percent increase in the length of the arc.

`\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}`

♥️
`\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}`