Final Answer:
The number of vehicles has been growing at 44 a year, while be bobuiation hai been growing at 19% a year. (a) Formula for the number of vehicles (in millions) as a function of t:
![\[ V(t) = 200 * e^(0.44t) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/38rco3q0cah00t5c4fae2kquimqu72fh81.png)
Step-by-step explanation:
The formula for exponential growth is given by
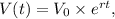 where
where
 is the initial amount,
is the initial amount,
 is the growth rate, and
is the growth rate, and
 is time in years. In this case,
is time in years. In this case,
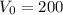 million vehicles, and the growth rate is 44% per year, so
million vehicles, and the growth rate is 44% per year, so
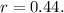 Substituting these values in, we get
Substituting these values in, we get
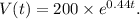
(b) Formula for the number of people (in millions) as a function of t:
![\[ P(t) = 277 * (1 + 0.19)^t \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/qojqe39uzslrd0z6tntue3jg5ivkos8cl2.png)
The formula for exponential growth is
 , where
, where
 is the initial amount,
is the initial amount,
 is the growth rate, and
is the growth rate, and
 is time in years. In this case,
is time in years. In this case,
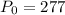 million people, and the growth rate is 19% per year, so
million people, and the growth rate is 19% per year, so
 Substituting these values in, we get
Substituting these values in, we get
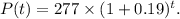
(c) To find when there is, on average, one vehicle per person, set
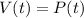 and solve for
and solve for
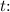
![\[ 200 * e^(0.44t) = 277 * (1 + 0.19)^t \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/dz1qw0ao4dhu8hey69ks89ixihmhbdnkbs.png)
Solving this equation for
 will give the number of years since 2000 when there is, on average, one vehicle per person. Unfortunately, this equation does not have a simple algebraic solution, and you may need to use numerical methods or a calculator to find the approximate value for
will give the number of years since 2000 when there is, on average, one vehicle per person. Unfortunately, this equation does not have a simple algebraic solution, and you may need to use numerical methods or a calculator to find the approximate value for
 .
.
Please note that the exact form of the solution is complex and may involve transcendental functions. The decimal form, rounded to the nearest tenth, would be the practical way to represent the solution.