Question

An input x(n)= [1, -3.5, 1.5] is given to a stable system. The output y(n)=[3, -4]. Determine the impulse response of the system using Z transform.

Answer 1

The impulse response of a system can be determined using the Z-transform by exploiting the relationship between the input and output signals. Let's denote the impulse response as
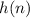`\displaystyle h(n)`, where
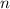`\displaystyle n` represents the discrete time index.

To find the impulse response, we need to establish the Z-transform relationship between the input
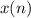`\displaystyle x(n)` and the output
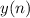`\displaystyle y(n)`. In this case, we know that the input
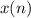`\displaystyle x(n)` is an impulse signal, which means it is nonzero only at
`\displaystyle n=0`.

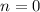Given that
`\displaystyle x(n) =[1, -3.5, 1.5]` and
`\displaystyle y(n) =[3, -4]`, we can set up the following equations:

`\displaystyle y(0) =h(0)x(0)`

`\displaystyle y(1) =h(0)x(1) +h(1)x(0)`

`\displaystyle y(2) =h(0)x(2) +h(1)x(1) +h(2)x(0)`

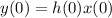
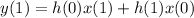
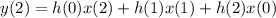
Plugging in the given values, we have:

`\displaystyle 3 =h(0)(1)`

`\displaystyle -4 =h(0)(-3.5) +h(1)(1)`

`\displaystyle 0 =h(0)(1.5) +h(1)(-3.5) +h(2)(1)`

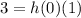
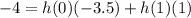
Simplifying these equations, we obtain:

`\displaystyle h(0) =3`

`\displaystyle -3.5h(0) +h(1) =-4`

`\displaystyle 1.5h(0) -3.5h(1) +h(2) =0`

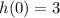
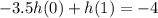
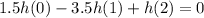
Now, let's represent these equations using the Z-transform. The Z-transform of a discrete-time signal
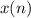`\displaystyle x(n)` is denoted as
`\displaystyle X(z)`, where
`\displaystyle z` represents the complex variable.

Applying the Z-transform to the equations, we have:

`\displaystyle 3 =h(0)(1)`

`\displaystyle -4 =h(0)(-3.5) +h(1)(1)`

`\displaystyle 0 =h(0)(1.5) -3.5h(1) +h(2)`

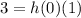
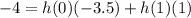
Now we can express these equations in terms of the Z-transformed variables:

`\displaystyle 3 =h(0) \cdot 1`

`\displaystyle -4 =h(0) \cdot (-3.5) +h(1) \cdot 1`

`\displaystyle 0 =h(0) \cdot 1.5 -3.5h(1) +h(2)`

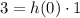
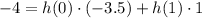
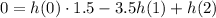
Simplifying further:

`\displaystyle 3 =h(0)`

`\displaystyle -4 =-3.5h(0) +h(1)`

`\displaystyle 0 =1.5h(0) -3.5h(1) +h(2)`

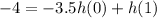
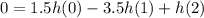
Now, we have a system of equations that we can solve to find the values of
`\displaystyle h(0)`,
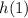`\displaystyle h(1)`, and
`\displaystyle h(2)`.

Solving the equations, we find:

`\displaystyle h(0) =3`

`\displaystyle h(1) =-2`

`\displaystyle h(2) =1`

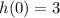
Therefore, the impulse response of the system is
`\displaystyle h(n) =[3, -2, 1]`.