Question

An analog signal is given as xa(t) = sin(480лt) + 6sin(420лt) which is sampled using Fs = 600 samples/sec. Compute the a. Nyquist sampling rate for xa(t), b. folding frequency, c. corresponding discrete time signal, d. frequencies of the corresponding discrete time signal, e. corresponding reconstructed signal ya(t) if it passes through an ideal D/A converter.

Answer 1

a. The Nyquist sampling rate for xa(t) can be calculated by taking twice the maximum frequency component in the signal. In this case, the maximum frequency component is 480л, so the Nyquist sampling rate is:

`\displaystyle \text{Nyquist sampling rate} = 2 * 480\pi = 960\pi \, \text{rad/sec}`

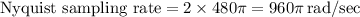
b. The folding frequency is equal to half the sampling rate. Since the sampling rate is 600 samples/sec, the folding frequency is:

`\displaystyle \text{Folding frequency} = (600)/(2) = 300 \, \text{Hz}`

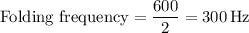
c. The corresponding discrete time signal can be obtained by sampling the analog signal at the given sampling rate. Using the sampling rate Fs = 600 samples/sec, we can sample the analog signal xa(t) as follows:

`\displaystyle xa[n] = xa(t) \Big|_(t=n/Fs) = \sin\left( 480\pi \cdot (n)/(600) \right) + 6\sin\left( 420\pi \cdot (n)/(600) \right)`

d. The frequencies of the corresponding discrete time signal can be determined by dividing the analog frequencies by the sampling rate. In this case, the discrete time signal frequencies are:

For the first term:
`\displaystyle (480\pi)/(600) = (4\pi)/(5)`

For the second term:
`\displaystyle (420\pi)/(600) = (7\pi)/(10)`

e. The corresponding reconstructed signal ya(t) can be obtained by applying an ideal digital-to-analog (D/A) converter to the discrete time signal. Since an ideal D/A converter perfectly reconstructs the original analog signal, ya(t) will be the same as xa(t):

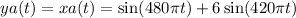
`\displaystyle ya(t) = xa(t) = \sin(480\pi t) + 6\sin(420\pi t)`

`\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}`

♥️
`\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}`