Question

A steel helical compression spring subjected to a maximum force of 2kN at a deflection of 25 mm. The maximum shearing stress is 500MPa and the number of inactive coils is 6 . The modulus of elasticity is 81GPa and the spring index is 4.5. Using SI units calculate: i) The actual size of the spring using the standard tables. ii) The volume of the spring.

Answer 1

i) To determine the actual size of the spring using standard tables, we need to calculate the spring constant (k) first.

The spring constant (k) can be calculated using Hooke's Law:

`\displaystyle F=k\cdot \delta`

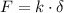
Where:

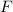`\displaystyle F` is the force applied (2 kN) and

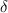`\displaystyle \delta` is the deflection (25 mm).

Converting the units to SI units:

`\displaystyle F=2\,\text{kN}=2* 10^(3)\,\text{N}`

`\displaystyle \delta =25\,\text{mm}=25* 10^(-3)\,\text{m}`

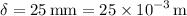
Substituting these values into the equation, we get:

`\displaystyle 2* 10^(3)\,\text{N}=k\cdot ( 25* 10^(-3)\,\text{m})`

Solving for
`\displaystyle k`:

`\displaystyle k=\frac{2* 10^(3)\,\text{N}}{25* 10^(-3)\,\text{m}}`

`\displaystyle k=80,000\,\text{N/m}`

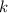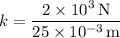
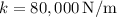
Now, to determine the actual size of the spring, we can use the spring constant and the spring index (C) given.

The spring index is defined as the ratio of the mean coil diameter (D) to the wire diameter (d). In this case, the spring index is given as 4.5.

`\displaystyle C=(D)/(d)=4.5`

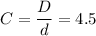
Rearranging the equation, we can solve for
`\displaystyle D`:

`\displaystyle D=C\cdot d`

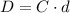
Substituting the spring index
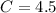`\displaystyle C=4.5`, we need to consult the standard tables to determine the appropriate wire diameter (d) for this spring index.

ii) To calculate the volume of the spring, we can use the formula for the volume of a cylinder:

`\displaystyle V=\pi \cdot r^(2) \cdot h`

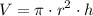
In this case, the spring can be approximated as a cylinder with a height (h) equal to the total length of the coils.

We need the mean coil diameter (D) and the wire diameter (d) to calculate the radius (r) of the cylinder.

Once we have the radius (r) and the height (h), we can substitute the values into the volume formula to calculate the volume of the spring.

`\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}`

♥️
`\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}`