Question

Please awnser I am
Stuck

Answer 1

`\textsf{(a)} \quad \textsf{B.\;\;To find the assets in 2013, subtitute $\boxed{13}$ for $x$ and evaluate to find $A(x)$.}`

`\textsf{In 2013 the assets are about \$ $\boxed{615.2}$\;billion.}`

`\textsf{(b)} \quad \textsf{A.\;\;To find the assets in 2016, subtitute $\boxed{16}$ for $x$ and evaluate to find $A(x)$.}`

`\textsf{In 2016 the assets are about \$ $\boxed{716.9}$\;billion.}`

`\textsf{(c)} \quad \textsf{A.\;\;To find the assets in 2019, subtitute $\boxed{19}$ for $x$ and evaluate to find $A(x)$.}`

`\textsf{In 2019 the assets are about \$ $\boxed{835.4}$\;billion.}`

Explanation:

The given function approximating the assets (in billions of dollars) for a financial firm is:

`A(x)=317e^(0.051x)`

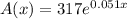
Given that x = 7 corresponds to the year 2007 then:

• x = 13 corresponds to the year 2013.
• x = 16 corresponds to the year 2016.
• x = 19 corresponds to the year 2019.

`\hrulefill`

Part (a)

B. To find the assets in 2013, substitute 13 for x and evaluate to find A(x).

`\begin{aligned}A(13)&=317e^(0.051\cdot 13)\\&=317e^(0.663)\\&=317 \cdot 1.940605...\\&=615.17192...\\&=615.2\end{aligned}`

In 2013 the assets are about $615.2 billion.

`\hrulefill`

Part (b)

A. To find the assets in 2016, substitute 16 for x and evaluate to find A(x).

`\begin{aligned}A(16)&=317e^(0.051\cdot 16)\\&=317e^(0.816)\\&=317 \cdot 2.261435...\\&=716.8752...\\&=716.9\end{aligned}`

In 2016 the assets are about $716.9 billion.

`\hrulefill`

Part (c)

A. To find the assets in 2019, substitute 19 for x and evaluate to find A(x).

`\begin{aligned}A(19)&=317e^(0.051\cdot 19)\\&=317e^(0.969)\\&=317 \cdot 2.635307...\\&=835.3925...\\&=835.4\end{aligned}`

In 2019 the assets are about $835.4 billion.