Question

Can anyone explain why the answer is B? Tyyy

Answer 1

B. 4.09 cm²

Explanation:

Let point O be the center of the circle.

As the center of the circle is the midpoint of the diameter, place point O midway between P and R.

Therefore, line segments OP and OQ are the radii of the circle.

As the radius (r) of a circle is half its diameter, r = OP = OQ = 5 cm.

As OP = OQ, triangle POQ is an isosceles triangle, where its apex angle is the central angle θ.

To calculate the shaded area, we need to subtract the area of the isosceles triangle POQ from the area of the sector of the circle POQ.

To do this, we first need to find the measure of angle θ by using the chord length formula:

`\boxed{\begin{minipage}{5.8 cm}\underline{Chord length formula}\\\\Chord length $=2r\sin\left((\theta)/(2)\right)$\\\\where:\\ \phantom{ww}$\bullet$ $r$ is the radius. \\ \phantom{ww}$\bullet$ $\theta$ is the central angle.\\\end{minipage}}`

Given the radius is 5 cm and the chord length PQ is 6 cm.

`\begin{aligned}\textsf{Chord length}&=2r\sin\left((\theta)/(2)\right)\\\\\implies 6&=2(5)\sin \left((\theta)/(2)\right)\\\\6&=10\sin \left((\theta)/(2)\right)\\\\(3)/(5)&=\sin \left((\theta)/(2)\right)\\\\(\theta)/(2)&=\sin^(-1) \left((3)/(5)\right)\\\\\theta&=2\sin^(-1) \left((3)/(5)\right)\\\\\theta&=73.73979529...^(\circ)\end{aligned}`

Therefore, the measure of angle θ is 73.73979529...°.

Next, we need to find the area of the sector POQ.

To do this, use the formula for the area of a sector.

`\boxed{\begin{minipage}{6.4 cm}\underline{Area of a sector}\\\\$A=\left((\theta)/(360^(\circ))\right) \pi r^2$\\\\where:\\ \phantom{ww}$\bullet$ $r$ is the radius. \\ \phantom{ww}$\bullet$ $\theta$ is the angle measured in degrees.\\\end{minipage}}`

Substitute θ = 73.73979529...° and r = 5 into the formula:

`\begin{aligned}\textsf{Area of section $POQ$}&=\left((73.73979529...^(\circ))/(360^(\circ))\right) \pi (5)^2\\\\&=0.20483... \cdot 25\pi\\\\&=16.0875277...\; \sf cm^2\end{aligned}`

Therefore, the area of sector POQ is 16.0875277... cm².

Now we need to find the area of the isosceles triangle POQ.

To do this, we can use the area of an isosceles triangle formula.

`\boxed{\begin{minipage}{6.7 cm}\underline{Area of an isosceles triangle}\\\\$A=(1)/(2)b\sqrt{a^2-(b^2)/(4)}$\\\\where:\\ \phantom{ww}$\bullet$ $a$ is the leg (congruent sides). \\ \phantom{ww}$\bullet$ $b$ is the base (side opposite the apex).\\\end{minipage}}`

The base of triangle POQ is the chord, so b = 6 cm.

The legs are the radii of the circle, so a = 5 cm.

Substitute these values into the formula:

`\begin{aligned}\textsf{Area of $\triangle POQ$}&=(1)/(2)(6)\sqrt{5^2-(6^2)/(4)}\\\\ &=3√(25-9)\\\\&=3√(16)\\\\&=3\cdot 4\\\\&=12\; \sf cm^2\end{aligned}`

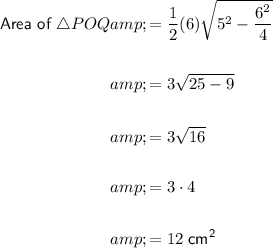
So the area of the isosceles triangle POQ is 12 cm².

Finally, to calculate the shaded area, subtract the area of the isosceles triangle from the area of the sector:

`\begin{aligned}\textsf{Shaded area}&=\textsf{Area of sector $POQ$}-\textsf{Area of $\triangle POQ$}\\\\&=16.0875277...-12\\\\&=4.0875277...\\\\&=4.09\; \sf cm^2\end{aligned}`

Therefore, the area of the shaded region is 4.09 cm².