Question

Optimal Chapter-Flight Fare If exactly 212 people sign up for a charter flight, Leisure World Travel Agency charges $292/person. However, if

more than 212 people sign up for the flight (assume this is the case), then each fare is reduced by $1 for each additional person. Determine how
many passengers will result in a maximum revenue for the travel agency. Hint: Let x denote the number of passengers above 212. Show that the
revenue function R is given by R(x) = (212+x)(292-x).
passengers
What is the maximum revenue?
$
What would be the fare per passenger in this case?
dollars per passenger

Answer 1

Dollars per passenger would be $252.
The maximum revenue is $63,404.

Explanation:

Let's define the number of passengers above 212 as x.

The revenue function is given by R(x) = (212 + x)(292 - x).

We can expand and simplify the revenue function:

`R(x) = 212 * 292 + 212 * (-x) + x * 292 + x * (-x)`

=
`61804 - 212x + 292x - x^2`

=
`-x^2 + 80x + 61804`

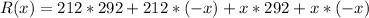
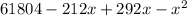
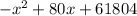
The revenue function is a quadratic function in the form
`R(x) = -x^2 + 80x + 61804`, representing a downward-opening parabola.

To find the x-coordinate of the vertex (which gives the number of passengers for maximum revenue), use the formula
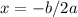`x = -b/2a`, where
`a = -1` and
`b = 80`.

`x=(-80)/(2*(-1))`

`= (80)/(2)`

`= 40`

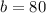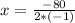
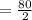
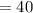
Therefore, the number of passengers above 212 for maximum revenue is 40.

Substitute x = 40 into the revenue function to find the maximum revenue:

`R(x) = -(40)^2 + 80(40) + 61804`

`= -1600 + 3200 + 61804`

`= 61804 + 1600`

`= 63404`

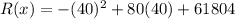
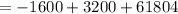
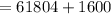
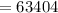
Hence, the maximum revenue is $63,404.

To determine the fare per passenger, subtract x from the base fare of $292:

Fare per passenger = Base fare - x

`= 292 - 40`

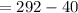
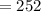`= 252` Dollars per passenger.