Question

1. Verify the following identity. (5 points) [1/tan(x)] + tan(x) = 1/[sin(x)cos(x)]

Answer 1

Certainly! Here is the verification of the given identity :

We need to verify the identity:

`\displaystyle (1)/(\tan(x)) + \tan(x) = (1)/(\sin(x)\cos(x))`.

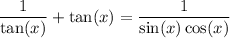To do this, let's start by expressing
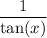`\displaystyle (1)/(\tan(x))` and
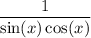`\displaystyle (1)/(\sin(x)\cos(x))` in terms of sine and cosine functions.

Recall that
`\displaystyle \tan(x) = (\sin(x))/(\cos(x))`.

Therefore,
`\displaystyle (1)/(\tan(x)) =(1)/((\sin(x))/(\cos(x))) = (\cos(x))/(\sin(x))`.

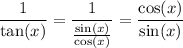Now, let's substitute these expressions into the given identity:

`\displaystyle (1)/(\tan(x)) + \tan(x) = (1)/(\sin(x)\cos(x))`.

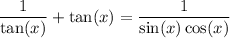Substituting
`\displaystyle (1)/(\tan(x)) = (\cos(x))/(\sin(x))`:

`\displaystyle (\cos(x))/(\sin(x)) + \tan(x) = (1)/(\sin(x)\cos(x))`.

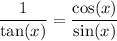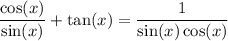To simplify the left side, we need a common denominator. The common denominator is
`\displaystyle \sin(x)\cos(x)`.

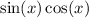So, we rewrite the left side:

`\displaystyle (\cos(x))/(\sin(x)) + \tan(x) = (\cos(x))/(\sin(x)) + (\sin(x))/(\cos(x))`.

Combining the fractions over the common denominator:

`\displaystyle (\cos(x) \cdot \cos(x) + \sin(x) \cdot \sin(x))/(\sin(x) \cdot \cos(x))`.

Using the Pythagorean identity
`\displaystyle \cos^2(x) + \sin^2(x) = 1`:

`\displaystyle (1)/(\sin(x) \cdot \cos(x))`.

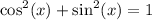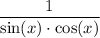Hence, we have shown that:

`\displaystyle (1)/(\tan(x)) + \tan(x) = (1)/(\sin(x) \cdot \cos(x))`.

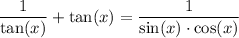Thus, the given identity has been verified.

`\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}`

♥️
`\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}`