Using Maxwell's equations, we can determine the magnetic flux density. One of the Maxwell's equations is:
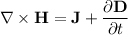 ,
,
where
 is the curl of the magnetic field intensity
is the curl of the magnetic field intensity
 ,
,
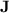 is the current density, and
is the current density, and
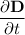 is the time derivative of the electric displacement
is the time derivative of the electric displacement
 .
.
In this problem, there is no current density (
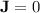 ) and no time-varying electric displacement (
) and no time-varying electric displacement (
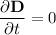 ). Therefore, the equation simplifies to:
). Therefore, the equation simplifies to:
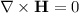 .
.
Taking the curl of the given magnetic field intensity
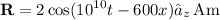 :
:
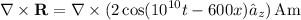 .
.
Using the curl identity and applying the chain rule, we can expand the expression:
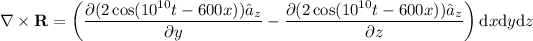 .
.
Since the magnetic field intensity
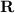 is not dependent on
is not dependent on
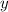 or
or
 , the partial derivatives with respect to
, the partial derivatives with respect to
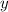 and
and
 are zero. Therefore, the expression further simplifies to:
are zero. Therefore, the expression further simplifies to:
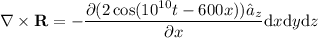 .
.
Differentiating the cosine function with respect to
 :
:
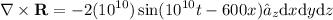 .
.
Setting this expression equal to zero according to
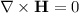 :
:
 .
.
Since the equation should hold for any arbitrary values of
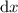 ,
,
 , and
, and
 , we can equate the coefficient of each term to zero:
, we can equate the coefficient of each term to zero:
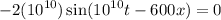 .
.
Simplifying the equation:
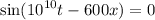 .
.
The sine function is equal to zero at certain values of
 :
:
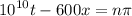 ,
,
where
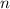 is an integer. Rearranging the equation:
is an integer. Rearranging the equation:
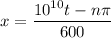 .
.
The equation provides a relationship between
 and
and
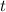 , indicating that the magnetic field intensity is constant along lines of constant
, indicating that the magnetic field intensity is constant along lines of constant
 and
and
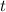 . Therefore, the magnetic field intensity is uniform in the given medium.
. Therefore, the magnetic field intensity is uniform in the given medium.
Since the magnetic flux density
 is related to the magnetic field intensity
is related to the magnetic field intensity
 through the equation
through the equation
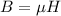 , where
, where
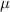 is the permeability of the medium, we can conclude that the magnetic flux density is also uniform in the medium.
is the permeability of the medium, we can conclude that the magnetic flux density is also uniform in the medium.
Thus, the correct expression for the magnetic flux density in the given medium is:
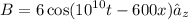 .
.