Question

Diego needs to install a support beam to hold up his new birdhouse, as modeled below. The

base of the birdhouse is 24 inches long. The support beam will form an angle of 38° with the
vertical post. Determine and state the approximate length of the support beam, x, to the
nearest inch.

Answer 1

To determine the length of the support beam, we can use trigonometric functions.

Let's consider the right triangle formed by the support beam, the vertical post, and the base of the birdhouse. The angle between the support beam and the vertical post is 38°.

In a right triangle, the trigonometric function we can use is the cosine function:

`\displaystyle \cos (\text{{angle}}) = \frac{{\text{{adjacent}}}}{{\text{{hypotenuse}}}}`

In this case, the adjacent side is the length of the base of the birdhouse, and the hypotenuse is the length of the support beam.

`\displaystyle \cos (38\degree ) = \frac{{24 \text{{ inches}}}}{{x}}`

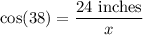
To find the length of the support beam, we can rearrange the equation:

`\displaystyle x = \frac{{24 \text{{ inches}}}}{{\cos (38\degree )}}`

Using a calculator, we can evaluate the cosine of 38°:

`\displaystyle \cos (38\degree ) \approx 0.788`

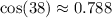
Substituting this value into the equation:

`\displaystyle x = \frac{{24 \text{{ inches}}}}{{0.788}}`

`\displaystyle x \approx 30.46 \text{{ inches}}`

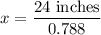
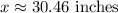
Rounding the length of the support beam to the nearest inch, we get:

Approximate length of the support beam,
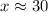`\displaystyle x \approx 30` inches.

`\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}`

♥️
`\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}`