1 Answer

Lacobus · Answer 1 · 2024-10-29T06:18:08+0000

To solve the inequality
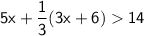$\displaystyle \sf 5x+(1)/(3)(3x+6)>14$ for x, we can simplify the expression and isolate x.

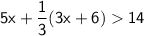
$\displaystyle \sf 5x+(1)/(3)(3x+6)>14$

To simplify the equation, we distribute
$\displaystyle \sf (1)/(3)$ to
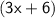$\displaystyle \sf ( 3x+6)$ :

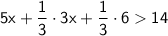
$\displaystyle \sf 5x+(1)/(3)\cdot 3x+(1)/(3)\cdot 6>14$

Simplifying further:

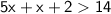
$\displaystyle \sf 5x+x+2>14$

Combining like terms:

$\displaystyle \sf 6x+2>14$

Next, we isolate x by subtracting 2 from both sides:

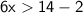
$\displaystyle \sf 6x>14-2$

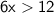
$\displaystyle \sf 6x>12$

Finally, we divide both sides of the inequality by 6 to solve for x:

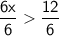
$\displaystyle \sf (6x)/(6)>(12)/(6)$

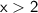
$\displaystyle \sf x>2$

Therefore, the solution to the inequality
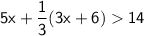$\displaystyle \sf 5x+(1)/(3)(3x+6)>14$ is
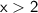$\displaystyle \sf x>2$ .

$\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}$

♥️
$\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}$

Please log in or register to add a comment.