Question

The linear transformation T: R3 → R2 is defined by T(x) = AX, where - A= -=[ 0 - 2 6 ]

[10 0 13 ] Find Ker(T). {(-13, 30, 10)} {(-13t, 30t, 10t), t ∈R} {(-13t, 30t, -10t), t∈R} {(13t, 30t, -10t), t∈R}

Answer 1

To find the kernel (null space) of the linear transformation T:
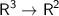`\displaystyle\sf R^(3)\rightarrow R^(2)`, defined by
`\displaystyle\sf T(x)=Ax`, where
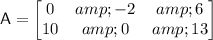`\displaystyle\sf A=\begin{bmatrix} 0 & -2 & 6 \\ 10 & 0 & 13 \end{bmatrix}`, we need to solve the equation
`\displaystyle\sf T(x)=0`.

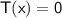Using
`\displaystyle\sf` tags for formatting, the matrix equation can be represented as:

`\displaystyle\sf A\begin{bmatrix} x_(1) \\ x_(2) \\ x_(3) \end{bmatrix}= \begin{bmatrix} 0 \\ 0 \end{bmatrix}`

Substituting the values of
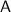`\displaystyle\sf A`, we have:

`\displaystyle\sf \begin{bmatrix} 0 & -2 & 6 \\ 10 & 0 & 13 \end{bmatrix}\begin{bmatrix} x_(1) \\ x_(2) \\ x_(3) \end{bmatrix}= \begin{bmatrix} 0 \\ 0 \end{bmatrix}`

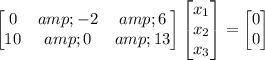
To find the kernel, we need to solve the augmented matrix
`\displaystyle\sf [A|0]` using row reduction techniques:

`\displaystyle\sf \begin{bmatrix} 0 & -2 & 6 & 0 \\ 10 & 0 & 13 & 0 \end{bmatrix}`

Performing row reduction, we get:

`\displaystyle\sf \begin{bmatrix} 10 & 0 & 13 & 0 \\ 0 & -2 & 6 & 0 \end{bmatrix}`

Dividing the first row by 10 and the second row by -2, we have:

`\displaystyle\sf \begin{bmatrix} 1 & 0 & (13)/(10) & 0 \\ 0 & 1 & -3 & 0 \end{bmatrix}`

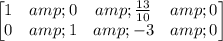
From the row-reduced form, we can see that
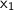`\displaystyle\sf x_(1)` and
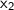`\displaystyle\sf x_(2)` are leading variables, while
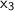`\displaystyle\sf x_(3)` is a free variable.

Therefore, the kernel (null space) of the transformation T is given by:

`\displaystyle\sf \begin{bmatrix} x_(1) \\ x_(2) \\ x_(3) \end{bmatrix}= \begin{bmatrix} -(13)/(10)x_(3) \\ 3x_(3) \\ x_(3) \end{bmatrix}`

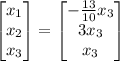
In set notation, we can represent the kernel as:

`\displaystyle\sf \text{Ker}(T)=\left\{ \left( -(13)/(10) t, 3t, t \right) \ \middle|\ t\in \mathbb{R} \right\}`

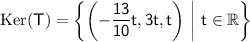
Therefore, the correct option is:
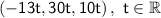`\displaystyle\sf \left( -13t, 30t, 10t \right),\ t\in \mathbb{R}`.