Question

Example-10: (Tubular Heat Exchanger) A heat exchanger is to cool ethylene (c, = 2.56 kJ /kg. °C) flowing at a rate of 2 kg/s from 80°C to 40°C by water (c, = 4.18 kJ/kg.°C) glycol that enters at 20°C and leaves at 55°C. Determine: a) The rate of heat transfer (Answer: 204.8 kW) b) The mass flow rate of water (Answer: 1.4 kg/sec)

Answer 1

a) To determine the rate of heat transfer in the tubular heat exchanger, we can use the equation:

`\displaystyle Q = \dot{m}_1 \cdot c_(p1) \cdot (T_{1,\text{in}} - T_{1,\text{out}})`,

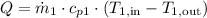where
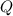`\displaystyle Q` is the rate of heat transfer,
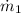`\displaystyle \dot{m}_1` is the mass flow rate of ethylene,
`\displaystyle c_(p1)` is the specific heat capacity of ethylene,
`\displaystyle T_{1,\text{in}}` is the inlet temperature of ethylene, and
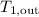`\displaystyle T_{1,\text{out}}` is the outlet temperature of ethylene.

Given:

`\displaystyle \dot{m}_1 = 2 \, \text{kg/s}`,

`\displaystyle c_(p1) = 2.56 \, \text{kJ/kg.°C}`,

`\displaystyle T_{1,\text{in}} = 80 \, \text{°C}`,

`\displaystyle T_{1,\text{out}} = 40 \, \text{°C}`.

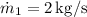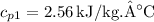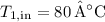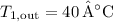Substituting these values into the equation, we can calculate the rate of heat transfer:

`\displaystyle Q = 2 \cdot 2.56 \cdot (80 - 40) \, \text{kW}`,

`\displaystyle Q = 204.8 \, \text{kW}`.

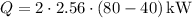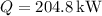Therefore, the rate of heat transfer in the tubular heat exchanger is 204.8 kW.

b) To determine the mass flow rate of water, we can use the equation:

`\displaystyle Q = \dot{m}_2 \cdot c_(p2) \cdot (T_{2,\text{out}} - T_{2,\text{in}})`,

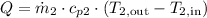where
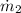`\displaystyle \dot{m}_2` is the mass flow rate of water,
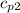`\displaystyle c_(p2)` is the specific heat capacity of water,
`\displaystyle T_{2,\text{in}}` is the inlet temperature of water, and
`\displaystyle T_{2,\text{out}}` is the outlet temperature of water.

Given:

`\displaystyle Q = 204.8 \, \text{kW}`,

`\displaystyle c_(p2) = 4.18 \, \text{kJ/kg.°C}`,

`\displaystyle T_{2,\text{in}} = 20 \, \text{°C}`,

`\displaystyle T_{2,\text{out}} = 55 \, \text{°C}`.

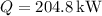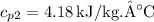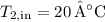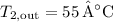Substituting these values into the equation, we can calculate the mass flow rate of water:

`\displaystyle 204.8 = \dot{m}_2 \cdot 4.18 \cdot (55 - 20) \, \text{kW}`,

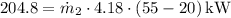Simplifying the equation:

`\displaystyle \dot{m}_2 = (204.8)/(4.18 \cdot 35) \, \text{kg/s}`,

`\displaystyle \dot{m}_2 \approx 1.4 \, \text{kg/s}`.

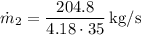Therefore, the mass flow rate of water in the tubular heat exchanger is approximately 1.4 kg/s.

`\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}`

♥️
`\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}`