Question

The point P(3,5) is rotated 180 degrees CW about the point A(3,2) and then rotated 90 degrees CCW about point B(1,1). What is the coordinate of P after the rotations?​

Answer 1

To determine the coordinate of point P after the described rotations, let's go step by step.

First, the point P(3, 5) is rotated 180 degrees clockwise about the point A(3, 2). To perform this rotation, we need to find the vector between the center of rotation (A) and the point being rotated (P). We can then apply the rotation matrix to obtain the new position.

Let
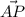`\vec{AP}` be the vector from A to P. We can calculate it as follows:

`\vec{AP} = \begin{bmatrix} 3 \\ 5 \end{bmatrix} - \begin{bmatrix} 3 \\ 2 \end{bmatrix} = \begin{bmatrix} 0 \\ 3 \end{bmatrix}`.

Now, we can apply the rotation matrix for a 180-degree clockwise rotation:

`\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}`,

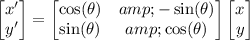where
`\theta` is the angle of rotation in radians. Since we want to rotate 180 degrees, we have
`\theta = \pi`.

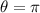Applying the rotation matrix, we get:

`\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} \cos(\pi) & -\sin(\pi) \\ \sin(\pi) & \cos(\pi) \end{bmatrix} \begin{bmatrix} 0 \\ 3 \end{bmatrix} = \begin{bmatrix} -1 & 0 \\ 0 & -1 \end{bmatrix} \begin{bmatrix} 0 \\ 3 \end{bmatrix} = \begin{bmatrix} 0 \\ -3 \end{bmatrix}`.

The new position of P after the first rotation is P'(0, -3).

Next, we need to rotate P' (0, -3) 90 degrees counterclockwise about the point B(1, 1).

Again, we calculate the vector from B to P', denoted as
`\vec{BP'}`:

`\vec{BP'} = \begin{bmatrix} 0 \\ -3 \end{bmatrix} - \begin{bmatrix} 1 \\ 1 \end{bmatrix} = \begin{bmatrix} -1 \\ -4 \end{bmatrix}`.

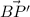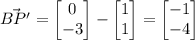Using the rotation matrix, we rotate
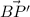`\vec{BP'}` by 90 degrees counterclockwise:

`\begin{bmatrix} x'' \\ y'' \end{bmatrix} = \begin{bmatrix} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{bmatrix} \begin{bmatrix} x' \\ y' \end{bmatrix}`,

where
`\theta` is the angle of rotation in radians. Since we want to rotate 90 degrees counterclockwise, we have
`\theta = (\pi)/(2)`.

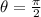Using the rotation matrix, we get:

`\begin{bmatrix} x'' \\ y'' \end{bmatrix} = \begin{bmatrix} \cos \left((\pi)/(2)\right) & -\sin\left((\pi)/(2)\right) \\ \sin\left((\pi)/(2)\right) & \cos\left((\pi)/(2)\right) \end{bmatrix} \begin{bmatrix} -1 \\ -4 \end{bmatrix} = \begin{bmatrix} 0 & -1 \\ 1 & 0\end{bmatrix} \begin{bmatrix} -1 \\ -4 \end{bmatrix} = \begin{bmatrix} 4 \\ -1 \end{bmatrix}`.

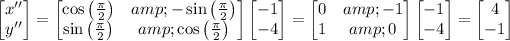The final position of P after both rotations is P''(4, -1).

Therefore, the coordinate of point P after the rotations is (4, -1).