The equation you provided is missing some closing brackets and exponents. Here is the corrected equation:
![\displaystyle \text{Electric field inside a plasma: } \vec{E}(\vec{r}) = -(q)/(4\pi\varepsilon_(0)\kappa) \left[\frac{e^{-(r)/(\lambda_(D))}}{r^(2)}+\frac{e^{-(r)/(\lambda_(D))}}{\lambda_(D) r}\right] \hat{r} = kq\left[\frac{e^{-(r)/(\lambda_(D))}}{r^(2)}+\frac{e^{-(r)/(\lambda_(D))}}{\lambda_(D) r}\right] \hat{r}](https://img.qammunity.org/2024/formulas/physics/high-school/s6tsdct2f2vxuzdyyg03raywz2qq3mz1cm.png)
Please note that the equation assumes the presence of charged particles inside a plasma and describes the electric field at a specific position
 . The terms
. The terms
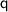 ,
,
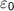 ,
,
 ,
,
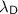 , and
, and
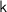 represent the charge of the particle, vacuum permittivity, dielectric constant, Debye length, and Coulomb's constant, respectively.
represent the charge of the particle, vacuum permittivity, dielectric constant, Debye length, and Coulomb's constant, respectively.
♥️