Use the Midpoint Rule with n=5 to estimate the volume obtained by rotating about the y-axis the region under the curve y=√(1+x^3), 0\leq x\leq 1.

Question

Use the Midpoint Rule with
`n=5` to estimate the volume obtained by rotating about the y-axis the region under the curve
`y=√(1+x^3)`,
`0\leq x\leq 1`.

Answer 1

The answer your looking for is right above my

Answer 2

To estimate the volume using the Midpoint Rule with
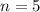`\displaystyle n=5`, we need to divide the interval
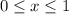`\displaystyle 0\leq x\leq 1` into
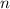`\displaystyle n` subintervals of equal width. Since
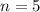`\displaystyle n=5`, each subinterval will have a width of
`\displaystyle \Delta x=(1-0)/(5)=(1)/(5)`.

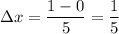Now, let's calculate the volume using the Midpoint Rule. The formula for the volume obtained by rotating about the y-axis is:

`\displaystyle V\approx 2\pi \sum _(i=1)^(n)y_(i)\Delta x`

where
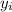`\displaystyle y_(i)` represents the value of the function
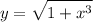`\displaystyle y=\sqrt{1+x^(3)}` evaluated at the midpoint of each subinterval.

First, let's find the midpoints of the subintervals. Since the width of each subinterval is
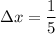`\displaystyle \Delta x=(1)/(5)`, the midpoint of the
`\displaystyle i`-th subinterval is given by:

`\displaystyle x_(i)=(\Delta x)/(2)+\left( i-(1)/(2)\right) \Delta x=(1)/(10)+\left( i-(1)/(2)\right) (1)/(5)`

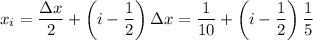
Substituting
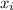`\displaystyle x_(i)` into the function
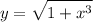`\displaystyle y=\sqrt{1+x^(3)}`, we obtain:

`\displaystyle y_(i)=\sqrt{1+\left( (1)/(10)+\left( i-(1)/(2)\right) (1)/(5)\right) ^(3)}`

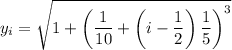
Now, we can calculate the approximate volume using the Midpoint Rule:

`\displaystyle V\approx 2\pi \sum _(i=1)^(5)y_(i)\Delta x`

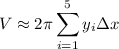
Substituting the values of
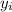`\displaystyle y_(i)` and
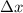`\displaystyle \Delta x` into the formula, we can evaluate the sum and compute the estimated volume.

`\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}`

♥️
`\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}`