Question

X^2+y^2-12y-12 ≤0
Find Center/Radius of Circle

Answer 1

To find the center and radius of the circle represented by the inequality
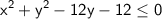`\displaystyle \sf x^(2) +y^(2) -12y-12\leq 0`, we can complete the square for the y terms.

The inequality can be rewritten as:

`\displaystyle \sf x^(2) +( y^(2) -12y) -12\leq 0`

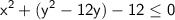
To complete the square for the y terms, we need to add and subtract
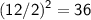`\displaystyle \sf ( 12/2) ^(2) =36` inside the parentheses:

`\displaystyle \sf x^(2) +( y^(2) -12y+36) -36-12\leq 0`

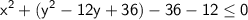
Simplifying, we have:

`\displaystyle \sf x^(2) +( y-6)^(2) -48\leq 0`

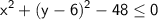
Now we can rewrite the inequality in the standard form of a circle equation:

`\displaystyle \sf ( x-h)^(2) +( y-k)^(2) \leq r^(2)`

Comparing this with the obtained equation, we can identify the center and radius of the circle:

Center:
`\displaystyle \sf ( h,k)=( 0,6)`

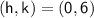
Radius:
`\displaystyle \sf r=√(48)`

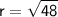
Therefore, the center of the circle is at
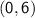`\displaystyle \sf ( 0,6)`, and its radius is
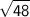`\displaystyle \sf √(48)`.

`\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}`

♥️
`\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}`