Question

A circle has a diameter with endpoints at A (-1. -9) and B (-11, 5). The point M (-6, -2) lies on the diameter. Prove or disprove that point M is the center of the circle by answering the following questions. Round answers to the nearest tenth (one decimal place). What is the distance from A to M? What is the distance from B to M? Is M the center of the circle? Yes or no?​

Answer 1

AM: 8.6 units

BM: 8.6 units

M is the center

Explanation:

Pre-Solving

We are given that the diameter of a circle is AB, where point A is at (-1, -9) and point B is (-11, 5).

We know that point M, which is at (-6, -2) is on AB. We want to know if it is the center of the circle.

If it is the center, then it means that the distance (measure) of AM is the same as the distance (measure) of BM.

Recall that the distance formula is
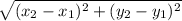`√((x_2-x_1)^2+(y_2-y_1)^2)`, where
`(x_1,y_1)` and
`(x_2,y_2)` are points.

Solving

Length of AM

The endpoints are point A and point M. We can label the values of the points to get:

`x_1=-1\\y_1=-9\\x_2=-6\\y_2=-2`

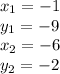
Now, plug them into the formula.

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

`d=√((-6--1)^2+(-2--9)^2)`

`d=√((-6+1)^2+(-2+9)^2)`

`d=√((-5)^2+(7)^2)`

`d=√(25+49)`

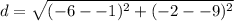
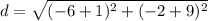
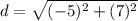
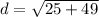
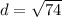`d=√(74)` ≈ 8.6 units

Length of BM

The endpoints are point B and point M. We can label the values and get:

`x_1=-11\\y_1=5\\x_2=-6\\y_2=-2`

Now, plug them into the formula.

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

`d=√((-6--11)^2+(-2-5)^2)`

`d=√((-6+11)^2+(-2-5)^2)`

`d=√((5)^2+(-7)^2)`

`d=√(25+49)`

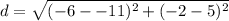
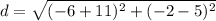
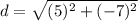
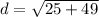
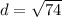`d=√(74)` ≈ 8.6 units.

Since the length of AM an BM are the same, M is the center of the circle.