Question

If you were given a quadratic function and a square root function, would the quadratic always be able to exceed the square root function? Explain your answer and offer mathematical evidence to support your claim.

Answer 1

No, a quadratic function will not always exceed a square root function. There are certain values of x where the square root function will be greater than the quadratic function.

Explanation:

The square root function is always increasing, while the quadratic function can be increasing, decreasing, or constant.

When the quadratic function is increasing, it will eventually exceed the square root function.

However, when the quadratic function is decreasing, it will eventually be less than the square root function.

Here is a mathematical example:

Quadratic function:
`f(x) = x^2`

Square root function:
`g(x) = \sqrt{x`

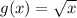
At x = 0, f(x) = 0 and g(x) = 0. Therefore, f(x) = g(x).

As x increases, f(x) increases faster than g(x). Therefore, f(x) will eventually exceed g(x).

At x = 4, f(x) = 16 and g(x) = 4. Therefore, f(x) > g(x).

As x continues to increase, f(x) will continue to increase, while g(x) will eventually decrease.

Therefore, there will be a point where f(x) will be greater than g(x).

In general, the quadratic function will exceed the square root function for sufficiently large values of x.

However, there will be a range of values of x where the square root function will be greater than the quadratic function.

Answer 2

No, a quadratic function does not always exceed a square root function. Whether a quadratic function exceeds a square root function depends on the specific equations of the functions and their respective domains. To provide a mathematical explanation, let's consider a specific example. Suppose we have the quadratic function f(x) = x^2 and the square root function g(x) = √x. We will compare these functions over a specific domain.

Let's consider the interval from x = 0 to x = 1. We can evaluate both functions at the endpoints and see which one is larger:

For f(x) = x^2:

f(0) = (0)^2 = 0

f(1) = (1)^2 = 1

For g(x) = √x:

g(0) = √(0) = 0

g(1) = √(1) = 1

As we can see, in this specific interval, the quadratic function and the square root function have equal values at both endpoints. Therefore, the quadratic function does not exceed the square root function in this particular case.

However, it's important to note that there may be other intervals or specific equations where the quadratic function does exceed the square root function. It ultimately depends on the specific equations and the range of values being considered.