Question

A rock of mass 0.298 kg falls from rest from a height of 23.1 m into a pail containing 0.304 kg of water. The rock and water have the same initial temperature. The specific heat capacity of the rock is 1880 J/(kg⋅C ∘

). Ignore the heat absorbed by the pail itself, and determine the rise in temperature of the rock and water in Celsius degrees. Number Units

Answer 1

Both the rock and the water will experience an approximate temperature rise of
`$0.123^(\circ) \mathrm{C}$`.

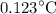To find the rise in temperature of the rock and water, we can use the principle of conservation of energy. The potential energy lost by the falling rock will be converted into the thermal energy gained by the rock and water.

The potential energy lost by the rock as it falls can be calculated using the formula:

`\[ \text{Potential energy} = \text{mass} * \text{gravity} * \text{height} \]`

The formula for potential energy is
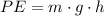`\(PE = m \cdot g \cdot h\)`, where:

• 
  `\(m\)` is the mass of the rock (0.298 kg)
• 
  `\(g\)` is the acceleration due to gravity (9.81 m/s²)
• 
  `\(h\)` is the height (23.1 m)

Let's calculate the potential energy lost by the rock:

`\[ PE = 0.298 \, \text{kg} * 9.81 \, \text{m/s}^2 * 23.1 \, \text{m} \]`

`\[ PE \approx 68.817 \, \text{J} \]`

This potential energy will be converted into the thermal energy gained by the rock and the water.

The thermal energy gained by the rock can be calculated using the specific heat formula:

`\[ \text{Thermal energy} = \text{mass} * \text{specific heat} * \Delta \text{temperature} \]`

Let (T) be the rise in temperature for both the rock and the water. The thermal energy gained by the rock and water will be:

For the rock:

`$68.817 \mathrm{~J}=0.298 \mathrm{~kg} * 1880 \mathrm{~J} /\left(\mathrm{kg} \cdot{ }^(\circ) \mathrm{C}\right) * T$`

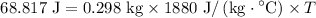
Solving for (T) (the rise in temperature of the rock):

`$\begin{aligned} & T \approx \frac{68.817 \mathrm{~J}}{0.298 \mathrm{~kg} * 1880 \mathrm{~J} /\left(\mathrm{kg} \cdot{ }^(\circ) \mathrm{C}\right)} \\ & T \approx 0.123{ }^(\circ) \mathrm{C}\end{aligned}$`

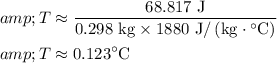
Therefore, The answer is
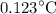`$0.123^(\circ) \mathrm{C}$`.

Answer 2

The rise in temperature of the rock and water is 0.04⁰ C.

How to calculate the rise in temperature?

The rise in temperature of the rock and water is calculated by applying the principle of conservation of energy as follows;

change in potential energy of the rock = heat absorbed by the rock and water

P.E = mgh

where;

• m is the mass of the rock
• h is the height of fall of the rock
• g is acceleration due to gravity

P.E = 0.298 kg x 9.8 m/s² x 23.1 m

P.E = 67.5 J

The rise in the temperature is calculated as;

P.E = Δθ (MC + mc)

67.5 = Δθ (0.298 x 1880 + 0.304 x 4186)

67.5 = Δθ (1,832.78)

Δθ = 67.5 / 1832.78

Δθ = 0.04⁰ C