Question

I'm not sure how to solve these types of questions, I need help. Thank you!

Answer 1

The x-intercept is (-5, 0).

The y-intercept is (0, 5).

Explanation:

To find the x-intercept, we set y = 0 and solve for x:

0 = 5 + x

x = -5

Therefore, the x-intercept is (-5, 0).

To find the y-intercept, we set x = 0 and solve for y:

y = 5 + 0

y = 5

Therefore, the y-intercept is (0, 5).

Answer 2

x-intercept is (-5,0)

y-intercept is (0,5)

Explanation:

We are given a linear equation and are asked to find the x- and y-intercepts of the equation.

`\Huge{y=5+x`

`\hrulefill`

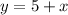
What are x- and y-intercepts?

In mathematics, the terms "x-intercept" and "y-intercept" refer to points where a graph intersects the x-axis and y-axis. They are important concepts in the study of functions and graphs.

The x-intercept is the point at which a graph crosses or intersects the x-axis. It represents the value of x when y is equal to zero. In other words, it is the value of x when the function or equation is satisfied with y = 0. The x-intercept is often denoted as (x, 0), where "x" is the x-coordinate of the point.

Similarly, the y-intercept is the point at which a graph crosses or intersects the y-axis. It represents the value of y when x is equal to zero. Geometrically, it is the point on the graph where x = 0. The y-intercept is often denoted as (0, y), where "y" is the y-coordinate of the point.
`\hrulefill`

(1) - Finding the x-intercept

To find the x-intercept, you set y equal to zero and solve the equation for x.

`y=5+x\\\\\\\text{Let y=0}\\\\\\\Longrightarrow 0=5+x\\\\\\\Longrightarrow \boxed{x=-5}`

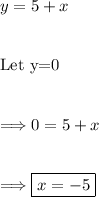
Thus, the x-intercept is (-5,0).

(2) - Finding the y-intercept

To find the y-intercept, you set x equal to zero and solve the equation for y.

`y=5+x\\\\\\\text{Let x=0}\\\\\\\Longrightarrow y=5+0\\\\\\\Longrightarrow \boxed{y=5}`

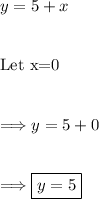
Thus, the y-intercept is (0,5).
`\hrulefill`

We can check this answer using a graphing calculator. Simply type in the given function and see were the function crosses each axis. Refer to the attached image.