Answer:
x = 2
Explanation:
Pre-Solving
We are given the following equation:
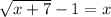 , which we want to solve for x.
, which we want to solve for x.
To do this, we should isolate the square root on one side, then square both sides. We can then solve the equation as normal, but then we have to check the domain in the end for any extraneous solutions.
Solving
Start by adding 1 to both sides.
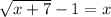
+1 +1
________________________
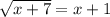
Now, square both sides.
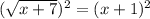
We get:
x + 7 = x² + 2x + 1
Subtract x + 7 from both sides.
x + 7 = x² + 2x + 1
-(x+7) -(x+7)
________________________
0 = x² + x - 6
This can be factored to become:
0 = (x+3)(x-2)
Solve:
x+3 = 0
x = -3
x-2 = 0
x = 2
We get x = -3 and x = 2. However, we must check the domain.
Domain
Substitute -3 as x and 2 as x into the original equation.
We get:
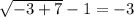
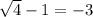
2 - 1 = -3
-1 = -3
This is an untrue statement, so x = -3 is an extraneous solution.
We also get:
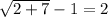
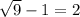
3 - 1 = 2
2 = 2
This is a true statement, so x = 2 is a real solution.
Our only answer is x = 2.