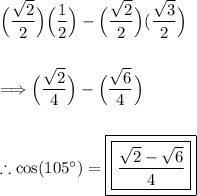Question

Find the exact value of cos 105⁰.

a. √√√2-√6
4
b.
√2+√6
4
C.
4
d. √2+√6
4

Answer 1

`(√(2)-√(6) )/(4) }`

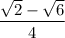
Explanation:

Find the exact value of cos(105°).

The method I am about to show you will allow you to complete this problem without a calculator. Although, memorizing the trigonometric identities and the unit circle is required.

We have,

`\cos(105\°)`

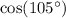
Using the angle sum identity for cosine.

`\boxed{\left\begin{array}{ccc}\text{\underline{Angle Sum Identity for Cosine}}\\\\\cos(A+B)=\cos(A)\cos(B)-\sin(A)\sin(B)\end{array}\right}`

Split the given angle, in degrees, into two angles. Preferably two angles we can recognize on the unit circle.

`105\textdegree=45\textdegree+60\textdegree\\\\\\\therefore \cos(105\textdegree)=\cos(45\textdegree+60\textdegree)`

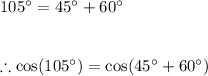
Now applying the identity.

`\cos(45\textdegree+60\textdegree)\\\\\\\Longrightarrow \cos(45\textdegree+60\textdegree)=\cos(45\textdegree)\cos(60\textdegree)-\sin(45\textdegree)\sin(60\textdegree)`

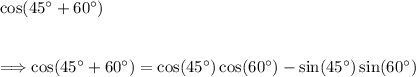
Now utilizing the unit circle.

`\boxed{\left\begin{array}{ccc}\text{\underline{From the Unit Circle:}}\\\\\cos(45\textdegree)=(√(2) )/(2)\\\\\cos(60\textdegree)=(1)/(2)\\\\\sin(45\textdegree)=(√(2) )/(2)\\\\\sin(60\textdegree)=(√(3) )/(2) \end{array}\right}`

`\cos(45\textdegree)\cos(60\textdegree)-\sin(45\textdegree)\sin(60\textdegree)\\\\\\\Longrightarrow \Big((√(2) )/(2)\Big)\Big((1 )/(2)\Big)-\Big((√(2) )/(2)\Big)((√(3) )/(2)\Big)`

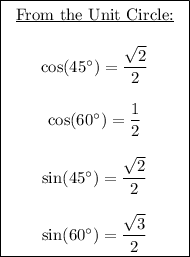
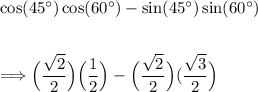
Now simplifying...

`\Big((√(2) )/(2)\Big)\Big((1 )/(2)\Big)-\Big((√(2) )/(2)\Big)((√(3) )/(2)\Big)\\\\\\\Longrightarrow \Big((√(2) )/(4) \Big)-\Big((√(6) )/(4) \Big)\\\\\\\therefore \cos(105\textdegree)= \boxed{\boxed{(√(2)-√(6) )/(4) }}`