Question

The professor knows that the speed of light, not love, is the only constant in the universe. The class boards a spaceship capable of travel at 0.8c.

a) If the ship was 150 m long when constructed, how long will it appear to the professor as they fly by at 0.8c?
b) the professor sets out in a backup ship to catch them. Relative to earth,

Answer 1

a) In special relativity, the length of an object moving relative to an observer appears shorter than its rest length due to the phenomenon known as length contraction. The formula for length contraction is given by:

L' =
`L * sqrt(1 - (v^2/c^2))`

Where:

L' is the length as observed by the professor,

L is the rest length of the ship (150 m),

v is the velocity of the ship (0.8c),

c is the speed of light.

Plugging in the values into the formula:

L' =
`150 * sqrt(1 - (0.8^2`

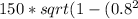
Calculating the expression inside the square root:

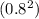`(0.8^2)` = 0.64

1 - 0.64 = 0.36

Taking the square root of 0.36:

sqrt(0.36) = 0.6

Finally, calculating the observed length:

L' = 150 * 0.6

L' = 90 m

Therefore, the ship will appear to the professor as 90 meters long as they fly by at 0.8c.

b) If the professor sets out in a backup ship to catch the original ship, relative to Earth, we can calculate the velocity of the professor's ship with respect to Earth using the relativistic velocity addition formula:

v' =
`(v1 + v2) / (1 + (v1 * v2) / c^2)`

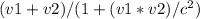
Where:

v' is the velocity of the professor's ship relative to Earth,

v1 is the velocity of the original ship (0.8c),

v2 is the velocity of the professor's ship (relative to the original ship),

c is the speed of light.

Assuming the professor's ship travels at 0.6c relative to the original ship:

v' = (0.8c + 0.6c) / (1 + (0.8c * 0.6c) / c^2)

v' = (1.4c) / (1 + 0.48)

v' = (1.4c) / 1.48

v' ≈ 0.9459c

Therefore, relative to Earth, the professor's ship will travel atapproximately 0.9459 times the speed of light.