Question

The mid-points of sides of a triangle are (3, 0), (4, 1) and (2, 1) respectively. Find the vertices of the triangle.​

Answer 1

(1, 0), (3, 2), (5, 0)

Explanation:

To find the vertices of the triangle given the midpoints of its sides, we can use the midpoint formula:

`\boxed{\begin{minipage}{7.4 cm}\underline{Midpoint between two points}\\\\Midpoint $=\left((x_2+x_1)/(2),(y_2+y_1)/(2)\right)$\\\\\\where $(x_1,y_1)$ and $(x_2,y_2)$ are the endpoints.\\\end{minipage}}`

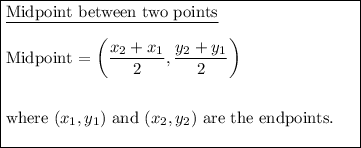
Let the vertices of the triangle be:

• 
  `A (x_A,y_A)`
• 
  `B (x_B,y_B)`
• 
  `C (x_C, y_C)`

Let the midpoints of the sides of the triangle be:

• D (2, 1) = midpoint of AB.
• E (4, 1) = midpoint of BC.
• F (3, 0) = midpoint of AC.

Since D is the midpoint of AB:

`\left((x_B+x_A)/(2),(y_B+y_A)/(2)\right)=(2,1)`

`\implies (x_B+x_A)/(2)=2 \qquad\textsf{and}\qquad (y_B+y_A)/(2)\right)=1`

`\implies x_B+x_A=4\qquad\textsf{and}\qquad y_B+y_A=2`

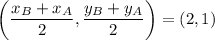
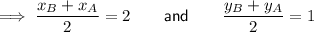
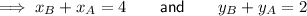
Since E is the midpoint of BC:

`\left((x_C+x_B)/(2),(y_C+y_B)/(2)\right)=(4,1)`

`\implies (x_C+x_B)/(2)=4 \qquad\textsf{and}\qquad (y_C+y_B)/(2)\right)=1`

`\implies x_C+x_B=8\qquad\textsf{and}\qquad y_C+y_B=2`

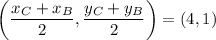
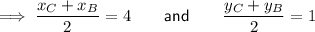
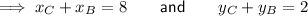
Since F is the midpoint of AC:

`\left((x_C+x_A)/(2),(y_C+y_A)/(2)\right)=(3,0)`

`\implies (x_C+x_A)/(2)=3 \qquad\textsf{and}\qquad (y_C+y_A)/(2)\right)=0`

`\implies x_C+x_A=6\qquad\textsf{and}\qquad y_C+y_A=0`

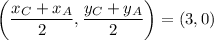
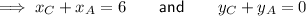
Add the x-value sums together:

`x_B+x_A+x_C+x_B+x_C+x_A=4+8+6`

`2x_A+2x_B+2x_C=18`

`x_A+x_B+x_C=9`

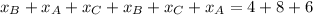
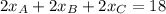
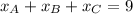
Substitute the x-coordinate sums found using the midpoint formula into the sum equation, and solve for the x-coordinates of the vertices:

`\textsf{As \;$x_B+x_A=4$, then:}`

`x_C+4=9\implies x_C=5`

`\textsf{As \;$x_C+x_B=8$, then:}`

`x_A+8=9 \implies x_A=1`

`\textsf{As \;$x_C+x_A=6$, then:}`

`x_B+6=9\implies x_B=3`

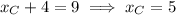
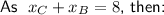
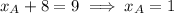
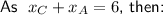
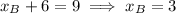
Add the y-value sums together:

`y_B+y_A+y_C+y_B+y_C+y_A=2+2+0`

`2y_A+2y_B+2y_C=4`

`y_A+y_B+y_C=2`

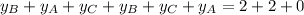
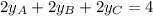
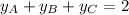
Substitute the y-coordinate sums found using the midpoint formula into the sum equation, and solve for the y-coordinates of the vertices:

`\textsf{As \;$y_B+y_A=2$, then:}`

`y_C+2=2\implies y_C=0`

`\textsf{As \;$y_C+y_B=2$, then:}`

`y_A+2=2 \implies y_A=0`

`\textsf{As \;$y_C+y_A=0$, then:}`

`y_B+0=2\implies y_B=2`

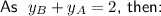
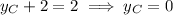
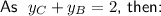
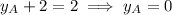
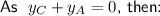
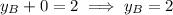
Therefore, the coordinates of the vertices A, B and C are:

• A (1, 0)
• B (3, 2)
• C (5, 0)