To find the value of the cosine of angle M in triangle AMNO, we can use the Law of Cosines. The Law of Cosines states that in a triangle with sides
 ,
,
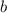 , and
, and
 , and angle
, and angle
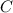 opposite side
opposite side
 , the following equation holds:
, the following equation holds:
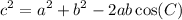
In triangle AMNO, we have the following information:
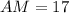 (side
(side
 )
)
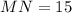 (side
(side
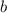 )
)
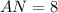 (side
(side
 )
)
Angle M = 90 degrees
We can apply the Law of Cosines to find the value of
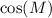 :
:
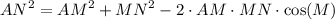
Substituting the given values:
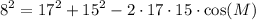
Simplifying:
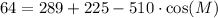
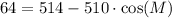
Rearranging the equation:
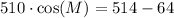

Dividing both sides by 510:
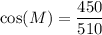
Simplifying:
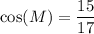
Therefore, the value of the cosine of angle M in triangle AMNO, to the nearest hundredth, is approximately
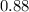 .
.
♥️