To determine the variable matrix
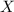 using the equation
using the equation
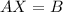 , we need to solve for
, we need to solve for
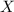 . We can do this by multiplying both sides of the equation by the inverse of matrix
. We can do this by multiplying both sides of the equation by the inverse of matrix
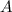 .
.
Let's start by finding the inverse of matrix
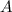 :
:

To find the inverse of matrix
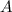 , we can use various methods such as the adjugate method or Gaussian elimination. In this case, we'll use the adjugate method.
, we can use various methods such as the adjugate method or Gaussian elimination. In this case, we'll use the adjugate method.
First, let's calculate the determinant of matrix
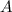 :
:
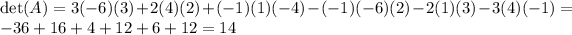
Next, let's find the matrix of minors:
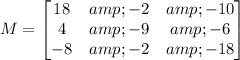
Then, calculate the matrix of cofactors:
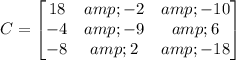
Next, let's find the adjugate matrix by transposing the matrix of cofactors:
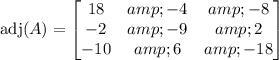
Finally, we can find the inverse of matrix
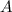 by dividing the adjugate matrix by the determinant:
by dividing the adjugate matrix by the determinant:

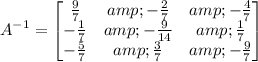
Now, we can find matrix
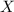 by multiplying both sides of the equation
by multiplying both sides of the equation
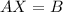 by the inverse of matrix
by the inverse of matrix
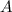 :
:

Substituting the given values:
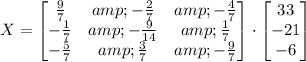
Calculating the multiplication, we get:
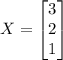
Therefore, the variable matrix
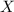 is:
is:
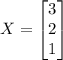

♥️
